
题目列表(包括答案和解析)
2.例二(P104-105 略)
1.若有向量 (
( ¹
¹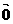 )、
)、 ,实数λ,使
,实数λ,使 =λ
=λ 则由实数与向量积的定义知:
则由实数与向量积的定义知: 与
与 为共线向量
为共线向量
若 与
与 共线(
共线( ¹
¹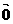 )且|
)且| |:|
|:| |=μ,则当
|=μ,则当 与
与 同向时
同向时 =μ
=μ
当 与
与 反向时
反向时 =-μ
=-μ
从而得:向量 与非零向量
与非零向量 共线的充要条件是:有且只有一个非零实数λ
共线的充要条件是:有且只有一个非零实数λ
使 =λ
=λ
4.例一 (见P104)略
3.运算定律:结合律:λ(μ )=(λμ)
)=(λμ) ①
①
第一分配律:(λ+μ) =λ
=λ +μ
+μ ②
②
第二分配律:λ( +
+ )=λ
)=λ +λ
+λ ③
③
结合律证明:
如果λ=0,μ=0, =
=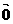 至少有一个成立,则①式成立
至少有一个成立,则①式成立
如果λ¹0,μ¹0, ¹
¹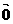 有:|λ(μ
有:|λ(μ )|=|λ||μ
)|=|λ||μ |=|λ||μ||
|=|λ||μ|| |
|
|(λμ) |=|λμ||
|=|λμ||  |=|λ||μ||
|=|λ||μ|| |
|
∴|λ(μ )|=|(λμ)
)|=|(λμ) |
|
如果λ、μ同号,则①式两端向量的方向都与 同向;
同向;
如果λ、μ异号,则①式两端向量的方向都与 反向。
反向。
从而λ(μ )=(λμ)
)=(λμ)
第一分配律证明:
如果λ=0,μ=0, =
=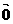 至少有一个成立,则②式显然成立
至少有一个成立,则②式显然成立
如果λ¹0,μ¹0, ¹
¹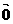
当λ、μ同号时,则λ 和μ
和μ 同向,
同向,
∴|(λ+μ) |=|λ+μ||
|=|λ+μ|| |=(|λ|+|μ|)|
|=(|λ|+|μ|)| |
|
|λ +μ
+μ |=|λ
|=|λ |+|μ
|+|μ |=|λ||
|=|λ|| |+|μ||
|+|μ|| |=(|λ|+|μ|)|
|=(|λ|+|μ|)| |
|
∵λ、μ同号 ∴②两边向量方向都与 同向
同向
即:|(λ+μ) |=|λ
|=|λ +μ
+μ |
|
当λ、μ异号,当λ>μ时 ②两边向量的方向都与λ 同向
同向
当λ<μ时 ②两边向量的方向都与μ 同向
同向
还可证:|(λ+μ) |=|λ
|=|λ +μ
+μ |
|
∴②式成立
第二分配律证明:
如果 =
=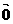 ,
, =
=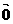 中至少有一个成立,或λ=0,λ=1则③式显然成立
中至少有一个成立,或λ=0,λ=1则③式显然成立
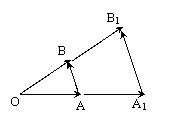 当
当 ¹
¹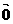 ,
, ¹
¹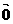 且λ¹0,λ¹1时
且λ¹0,λ¹1时
1°当λ>0且λ¹1时在平面内任取一点O,
作

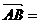

 λ
λ
 λ
λ
则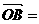
 +
+
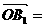 λ
λ +λ
+λ
由作法知: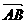 ∥
∥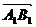 有ÐOAB=ÐOA1B1 |
有ÐOAB=ÐOA1B1 |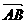 |=λ|
|=λ|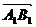 |
|
∴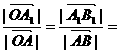 λ ∴△OAB∽△OA1B1
λ ∴△OAB∽△OA1B1
∴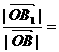 λ ÐAOB=Ð
A1OB1
λ ÐAOB=Ð
A1OB1
因此,O,B,B1在同一直线上,|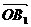 |=|λ
|=|λ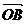 |
| 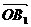 与λ
与λ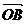 方向也相同
方向也相同
 λ(
λ( +
+ )=λ
)=λ +λ
+λ
当λ<0时 可类似证明:λ( +
+ )=λ
)=λ +λ
+λ
∴ ③式成立
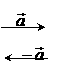
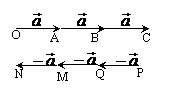
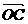 =
=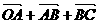 =
= +
+ +
+ =3
=3
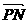 =
=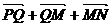 =(-
=(- )+(-
)+(- )+(-
)+(- )=-3
)=-3
讨论:1°3 与
与 方向相同且|3
方向相同且|3 |=3|
|=3| |
|
2°-3 与
与 方向相反且|-3
方向相反且|-3 |=3|
|=3| |
|
2.从而提出课题:实数与向量的积
实数λ与向量 的积,记作:λ
的积,记作:λ
定义:实数λ与向量 的积是一个向量,记作:λ
的积是一个向量,记作:λ
1°|λ |=|λ||
|=|λ|| |
|
2°λ>0时λ 与
与 方向相同;λ<0时λ
方向相同;λ<0时λ 与
与 方向相反;λ=0时λ
方向相反;λ=0时λ =
=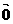
6.1kg的重物在两根细绳的支持下,处于平衡状态(如图),已知两细绳与水平线分别成30°, 60°角,问两细绳各受到多大的力?
解:将重力在两根细绳方向上分解,两细绳间夹角为90°
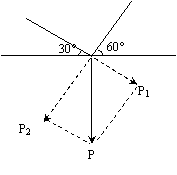
 =1 (kg) ÐP1OP=60° ÐP2OP=30°
=1 (kg) ÐP1OP=60° ÐP2OP=30°
∴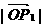 =
= cos60°=1•
cos60°=1• =0.5
(kg)
=0.5
(kg)
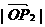 =
= cos30°=1•
cos30°=1•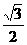 =0.87
(kg)
=0.87
(kg)
即两根细绳上承受的拉力分别为0.5 kg和0.87 kg
5.如图,已知梯形ABCD中,AB∥CD且AB=2CD,M, N分别是DC, AB中点,设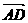 =
= ,
, 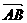 =
= ,试以
,试以 ,
,  为基底表示
为基底表示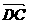 ,
,  ,
, 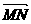
解: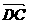 =
=
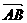 =
=
 连ND 则DC╩ND
连ND 则DC╩ND
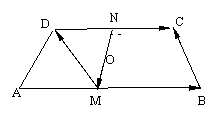 ∴
∴ =
=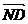 =
=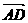 -
-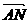 =
= -
-

又: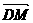 =
=
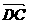 =
=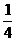

∴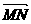 =
=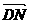 -
-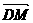 =
=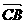 -
-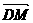 =-
=- -
-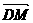
=(- +
+
 )-
)-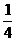
 =
=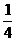
 -
-
4.设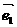 ,
, 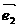 是两个不共线向量,已知
是两个不共线向量,已知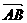 =2
=2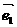 +k
+k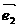 ,
, 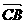 =
=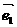 +3
+3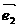 ,
, 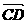 =2
=2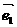 -
-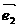 , 若三点A, B, D共线,求k的值。
, 若三点A, B, D共线,求k的值。
解: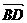 =
=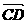 -
-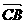 =(2
=(2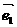 -
-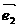 )-(
)-(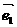 +3
+3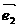 )=
)=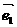 -4
-4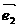
∵A, B, D共线 ∴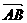 ,
,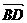 共线
∴存在λ使
共线
∴存在λ使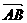 =λ
=λ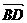
即2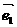 +k
+k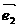 =λ(
=λ(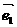 -4
-4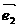 ) ∴
) ∴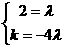 ∴k=-8
∴k=-8
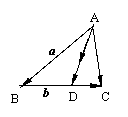
2.如图,在△ABC中, =
= ,
,  =
= AD为边BC的中线,G为△ABC的重心,求向量
AD为边BC的中线,G为△ABC的重心,求向量
解一:∵ =
= ,
,  =
= 则
则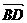 =
=
 =
=

 ∴
∴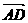 =
=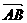 +
+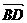 =
= +
+
 而
而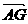 =
=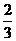
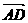
∴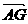 =
=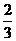
 +
+

解二:过G作BC的平行线,交AB、AC于E、F
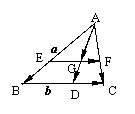 ∵△AEF∽△ABC
∵△AEF∽△ABC
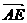 =
=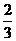
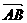 =
=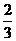

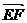 =
=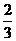
 =
=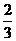

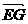 =
=
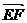 =
=

∴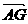 =
=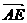 +
+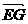 =
=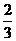
 +
+

 3.在 ABCD中,设对角线
3.在 ABCD中,设对角线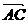 =
= ,
,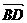 =
= 试用
试用 ,
,  表示
表示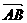 ,
,
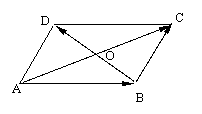 解一:
解一: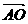 =
=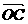 =
=

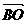 =
=
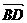 =
=

∴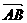 =
=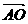 +
+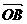 =
=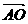 -
-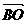 =
=
 -
-

 =
=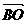 +
+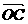 =
=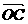 +
+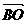 =
=
 +
+

解二:设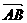 =
=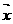 ,
, =
=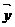
则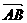 +
+ =
=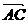
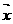 +
+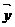 =
= ∴
∴ 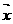 =
= (
( -
- )
)
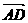 -
-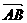 =
=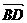
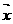 -
-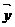 =
=
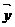 =
= (
( +
+ )
)
即: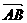 =
= (
( -
- )
)  =
= (
( +
+ )
)
1.当λÎZ时,验证:λ( +
+ )=λ
)=λ +λ
+λ
证:当λ=0时,左边=0•( +
+ )=
)=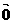 右边=0•
右边=0• +0•
+0• =
=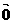 分配律成立
分配律成立
当λ为正整数时,令λ=n, 则有:
n( +
+ )=(
)=( +
+ )+(
)+( +
+ )+…+(
)+…+( +
+ )
)
= +
+ +…+
+…+ +
+ +
+ +
+ +…+
+…+ =n
=n +n
+n
即λ为正整数时,分配律成立
当为负整数时,令λ=-n(n为正整数),有
-n( +
+ )=n[-(
)=n[-( +
+ )]=n[(-
)]=n[(- )+(-
)+(- )]=n(-
)]=n(- )+n(-
)+n(- )=-n
)=-n +(-n
+(-n )=-n
)=-n -n
-n
分配律仍成立
综上所述,当λ为整数时,λ( +
+ )=λ
)=λ +λ
+λ 恒成立 。
恒成立 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com