
题目列表(包括答案和解析)
16、解析:由△=4(cosθ+1)2-4cos2θ≥0得cosθ≥-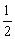 。
。
又α+β =-2(cosθ+1),α·β=cos2θ
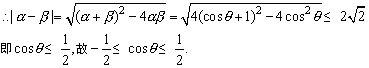
利用三角函数线可得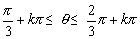 (k∈Z).
(k∈Z).
∴ 5°(x+T)+20°=5°·x+20°+k·360°
即 T=72k。
又∵ g(x+T)与g(x)终边相同,
∴ 6°·(x+T)+30°=6°x+30°+k′·360°.
即 T=60k′。
由于 60和72的最小公倍数是360,故T=360k(k∈Z).
15、解析:∵ θ在第四象限,∴ 0<cosθ<1<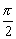 ,-
,-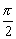 <-1<sinθ<0,
<-1<sinθ<0,
∴ sin(cosθ)>0,cos(sinθ)>0
∴ sin(cosθ)·cos(sinθ)>0.
13、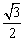
提示:从特殊看起,可得到 f(1)=f(7),f(2)=f(8),f(3)=f(9),…
∴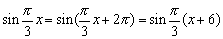
f(1)+f(2)+…+f(2005)=[f(1)+f(2)+…+f(6)]×334+f(2005)
而 f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=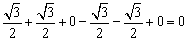 .
.
∴ f(1)+f(2)+…+f(2005)=f(2005)=f(1)=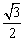 .
.
解:由三角函数的定义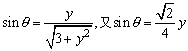 ,故y2=5.
,故y2=5.
∴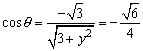 .
.
12、C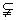 A
A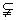 B
B
解析: A={α|α=2k·180°+60°,k∈Z},∴ A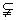 B
B
C={α|α=2k·360°+60°,k∈Z},∴ C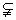 A,故C
A,故C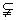 A
A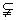 B.
B.
16、若α,β是关于x的二次方程,x2+2(cosθ+1)x+cos2θ=0的两根,且|α-β|≤2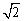 ,求θ的范围.
,求θ的范围.
答案:一、1---5CCBBC, 6---10ACBCA
15、若θ在第四象限,试判断sin(cosθ)·cos(sinθ)的符号.
14、已知f(x)=5°·x+20°,g(x)=6°x+30°,问T为何值时,对任意x值均有f(x+T)与f(x),g(x+T)与g(x)同时终边相同?
13、设f(x)=sin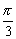 x,则f(1)+f(2)+f(3)+…+f(2005)=___________.
x,则f(1)+f(2)+f(3)+…+f(2005)=___________.
12、若A={α|α=60°+k·360°,k∈Z},B={α|α=60°+k·180°,k∈Z},C={α|α=60°+k·720°,k∈Z},则A、B、C的关系是___________.
11、已知角θ的终边上有一点P(-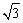 ,y)(y≠0)且sinθ=
,y)(y≠0)且sinθ=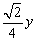 ,则cosθ=___________.
,则cosθ=___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com