
题目列表(包括答案和解析)
2. 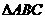 中,求证:
中,求证: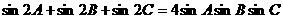
1. 已知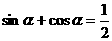 ,求值。
,求值。
(1)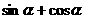 (2)
(2)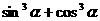
(3)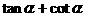 (4)
(4)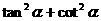
(5)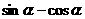
1.写出下式中,角α与角β的终边位置关系. (1)sinα=sinβ,则 . (2)cosα=cosβ,则 . (3)tgα=tgβ,则 .
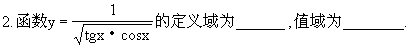

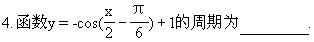
12.0≤θ<2π,sinθ<0且cos2θ<0,则θ是 [ ]
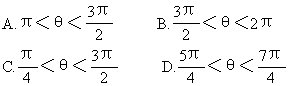
10.若函数y=sin(π+x),y=cos(2π-x)都是减函数,则x的集合是[ ]
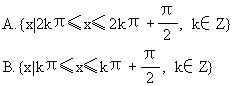
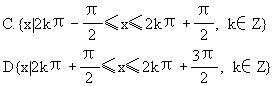

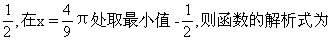 [ ]
[ ]
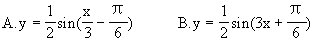

5.函数y=x3sinx+cos2x为 [ ] A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.既非奇函数又非偶函数
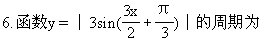 [ ]
[ ]
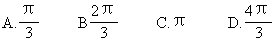
 [ ]
A.第一象限 B.第二象限 C.第三象限 D.第四象限
[ ]
A.第一象限 B.第二象限 C.第三象限 D.第四象限
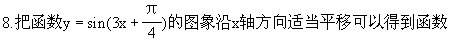 y=sin3x的图象,这种平移可以是 [ ]
y=sin3x的图象,这种平移可以是 [ ]
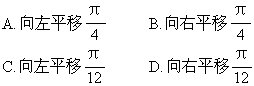
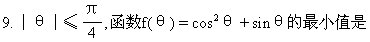 [ ]
[ ]
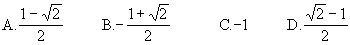
1.一个扇形OAB的面积是1cm2,它的周长是4cm,则它的中心角是 [ ] A.2弧度 B.3弧度 C.4弧度 D.5弧度
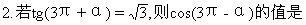 [ ]
[ ]
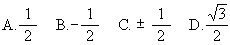
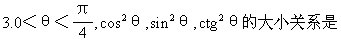 [ ]
A.cos2θ<sin2θ<ctg2θ B.ctg2θ<sin2θ<cos2θ
C.sin2θ<cos2θ<ctg2θ D.cos2θ<ctg2θ<sin2θ
[ ]
A.cos2θ<sin2θ<ctg2θ B.ctg2θ<sin2θ<cos2θ
C.sin2θ<cos2θ<ctg2θ D.cos2θ<ctg2θ<sin2θ
 [ ]
[ ]
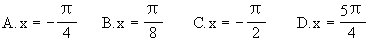
3. 解答题
(1)
解:令t=sinθ+cosθ 则-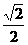 ?≤t≤1
?≤t≤1
∴2sinθcosθ=t2-1
∴y=t2-t-1=(t-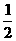 )2-
)2-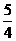
∴y∈[-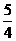 ,1]
,1]
(2)原式=2sinαcosβ+sinαsinβ-2cosαsinβ
=cosαcosβ(2tgα+tgαtgβ-2tgβ)
=cosαcosβ(2tg3525+log3525·log725-2log725)
=cosαcosβ[4log355+4log355·log75-4log75]
=cosαcosβ[4log355(1+log75)-4log75]
=cosαcosβ[4log355 ·log735-4log75]
=cosαcosβ(4log75-4log75)
=0
(3)解由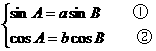 ①2+②2得a2sin2B+b2cos2B=1
①2+②2得a2sin2B+b2cos2B=1
∴cos2B= ∴sin2B=
∴sin2B= ∴tg2B=
∴tg2B=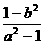
∵B为锐角 ∴tgB=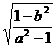
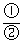 得tg A=
得tg A=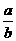 tgB=
tgB=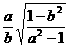
(4)解略:(1)α+β的值为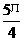
( 2 ) cos (α+β)=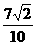
(5)解:∵B=60° ∴A+C=120° cos(A+C)=-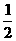
又由已知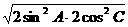 =
=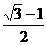
∴cosAcosC=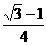 sinAsinC=
sinAsinC=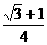
∴cos(C-A)= 即C-A=30°
即C-A=30°
∴A=45° B=60° C=75°
∴a+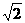 b=2R(sin45°+
b=2R(sin45°+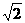 sin60°)
sin60°)
=2·2R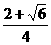 =2·2Rsin75°
=2·2Rsin75°
=2C
(6)解:∵2R=AD+DB AD=rtg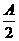
BD=rtg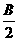
∴2R=r(tg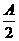 +tg
+tg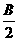 )
)
∴ 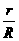 =
=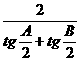 =
=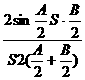
=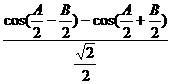
=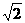 [cos(
[cos(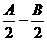 )-
)-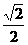 ]
]
≤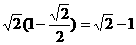
故当A=B时 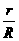 有最大值
有最大值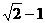
(7)解:由sinx+siny=sinxsiny可得
2sin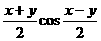 =-
=-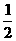 [cos(x+y)-cos(x-y)]
[cos(x+y)-cos(x-y)]
=-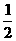 [(1-2sin2
[(1-2sin2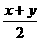 )-(2cos2
)-(2cos2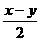 )-1]
)-1]
=-1+sin2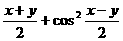
∴(sin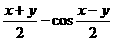 )2=1
)2=1
∴sin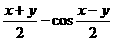 =±1
=±1
再由tg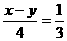 知cos
知cos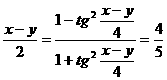
∴sin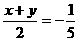 (
( >1舍去)
>1舍去)
(8)解:∵x1、x2是方程x-sin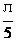 x1、x2
x1、x2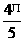
∴tg(α+β)=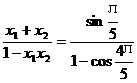
=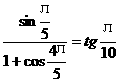
又由题意α、β中有一个在这间(-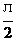 ,0)内
,0)内
∴-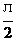 <α+β<
<α+β<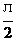 ∴α+β=
∴α+β=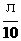
(9)解:由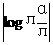 <1 知
<1 知
-1<logл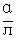 <1 即1<α<л2
<1 即1<α<л2
要使f (x)为偶数,必须f (-x)=f (x)
即x∈R恒成立
移项 和差化积得
2sinxcosα=-2sinxsinα
若对x∈R恒成立
必须:tgα=-1 ∴α=kл+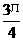 (k∈z)
(k∈z)
于是 1<kл+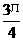 <л2
<л2
知 k=0,1,2
∴α=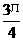 ,
,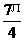 ,
,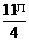
(10)解:设∠BAP=α α∈[0,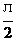 ]
]
∠BQP=β,在△PAB,△PBQ中
由余弦定理cosβ=cosα-1
∴S2+T2=( sinα)2+(
sinα)2+(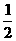 sinβ)2
sinβ)2
=-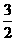 (cos-
(cos-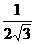 )2+
)2+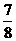
∴当cosα=1时,S2+T2有最小值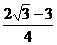
当cosα=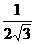 时,S2+T2有最大值
时,S2+T2有最大值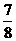
2. 填空题
(1)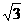 (2)
(2)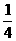 (3)
(3) (4)-
(4)- (5)正三角形 (6)2l(
(5)正三角形 (6)2l(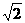 -1)
-1)
(7)-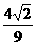 (8)①②③ (9)32 (10)
(8)①②③ (9)32 (10)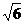
1. 选择题
C C B B C B B C B D C BCBD CBCDA C D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com