
题目列表(包括答案和解析)
x1x2+ y1y2=|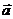 ||
||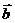 |cosq
|cosq
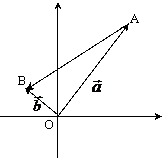 证:如图:设
证:如图:设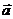 ,
, 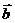 起点在原点,终点为A,B
起点在原点,终点为A,B
则A=(x1,
y1) B=(x2,
y2) 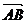 =
=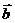 -
-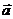
在△ABC中,由余弦定理
|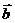 -
-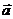 |2=|
|2=|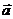 |2+|
|2+|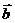 |2-2|
|2-2|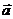 ||
||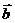 | cosq
| cosq
∵|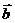 -
-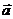 |2=|
|2=|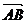 |2=|(x2-x1, y2-y1)|2=(x2-x1)2+(
y2-y1)2
|2=|(x2-x1, y2-y1)|2=(x2-x1)2+(
y2-y1)2
|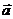 |2=x12+y12
|
|2=x12+y12
|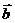 |2= x22+y22
|2= x22+y22
∴(x2-x1)2+(
y2-y1)2= x12+y12+
x22+y22-2|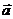 ||
||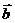 | cosq
| cosq
∴x1x2+
y1y2=|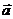 ||
||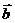 |cosq
即有
|cosq
即有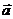 •
•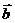 = x1x2+ y1y2=|
= x1x2+ y1y2=|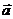 ||
||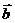 |cosq
|cosq
形(边长保留四个有效数字,角度精确到期1’)
解略
解略
能解决的问题:1.已知三边求角
2.已知三边和它们的夹角求第三边
3.强调几个问题:1°熟悉定理的结构,注意“平方”“夹角”“余弦”等
2°知三求一
3°当夹角为90°时,即三角形为直角三角形时即为勾股定理(特例)
4°变形: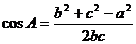
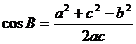
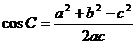
2.语言叙述:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。
1.余弦定理的向量证明:
设△ABC三边长分别为a, b, c
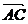 =
=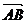 +
+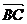
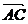 •
•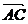 =(
=(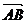 +
+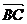 )•(
)•(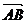 +
+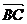 )=
)=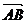 2+2
2+2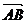 •
•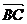 +
+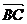 2
2
=| 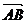 |2+2|
|2+2|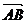 |•|
|•|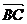 |cos(180°- B)+|
|cos(180°- B)+|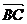 |2=
|2=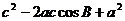
即: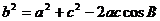
同理可得: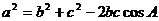
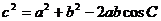
1.若 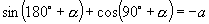 ,
则
,
则 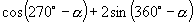 的值为( ).
A.
的值为( ).
A. 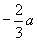 B.
B. 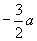 C.
C. 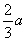 D.
D. 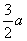 2.
2. 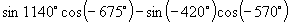 的值等于( ).
A.
的值等于( ).
A. 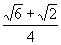 B.
B. 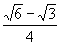 C.
C. 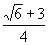 D.
D. 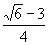 3.在△
3.在△ 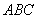 中,下列各表达式为常数的是( ).
A.
中,下列各表达式为常数的是( ).
A. 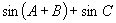 B.
B. 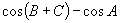 C.
C.  D.
D. 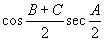 4.如果
4.如果 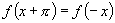 ,且
,且
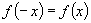 ,则
,则
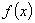 可以是( ).
A.
可以是( ).
A. 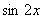 B.
B.  C.
C. 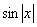 D.
D.  5.已知
5.已知 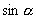 是方程
是方程
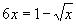 的根,那么
的根,那么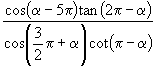 的值等于( ).
A.
的值等于( ).
A. 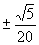 B.
B. 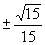 C.
C. 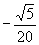 D.
D. 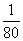 二、填空题
6.计算
二、填空题
6.计算 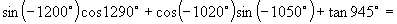 .
7.已知
.
7.已知 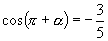 ,
,
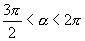 ,则
,则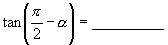 ,
,
 .
8.若
.
8.若 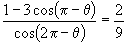 ,则
,则
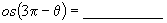 .
9.设
.
9.设 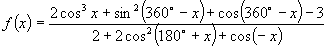 ,则
,则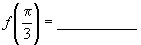 .
10.
.
10. 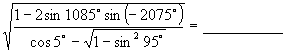 .
三、解答题
11.求值:
.
三、解答题
11.求值:
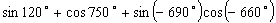
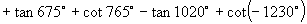 12.已知角
12.已知角 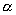 终边上一点
终边上一点
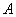 的坐标为
的坐标为
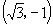 ,
(1)化简下列式子并求其值:
,
(1)化简下列式子并求其值: 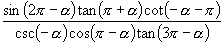 ;
(2)求角
;
(2)求角 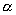 的集合.
13.已知
的集合.
13.已知 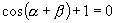 ,求证:
,求证:
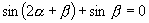 .
14.若
.
14.若 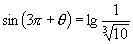 ,
求
,
求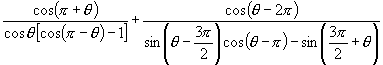 的值.
15.已知
的值.
15.已知 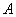 、
、
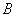 、
、
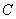 为△
为△ 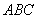 的内角,求证:
(1)
的内角,求证:
(1) 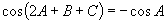 ;(2)
;(2) 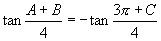 .
16.已知
.
16.已知 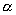 为锐角,并且
为锐角,并且
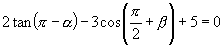 ,
,
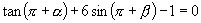 ,求
,求
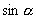 的值.
的值.
15、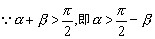
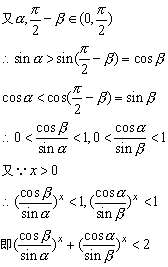
14、f(x)=4cos22x-8cos2x+3
(1)由f(x)﹥0得(2cos2x-3)(2cos2x-1)﹥0
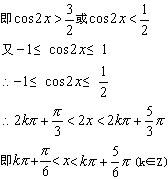
(2)f(x)=4(cos2x-1)2-1
当cos2x=1时,f(x)min=-1,此时x=kπ(k∈Z)
当cos2x=-1,即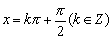 时,f(x)max=15.
时,f(x)max=15.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com