
题目列表(包括答案和解析)
2.用加法的逆运算定义向量的减法:
向量的减法是向量加法的逆运算:
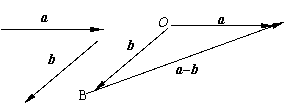 若b + x
= a,则x叫做a与b的差,记作a - b
若b + x
= a,则x叫做a与b的差,记作a - b
1.用“相反向量”定义向量的减法
1°“相反向量”的定义:与a长度相同、方向相反的向量。记作 -a
2°规定:零向量的相反向量仍是零向量。-(-a) = a
任一向量与它的相反向量的和是零向量。a + (-a) = 0
如果a、b互为相反向量,则a = -b, b = -a, a + b = 0
3°向量减法的定义:向量a加上的b相反向量,叫做a与b的差。
即:a - b = a + (-b) 求两个向量差的运算叫做向量的减法。
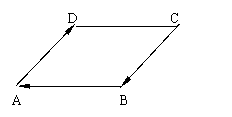 向量加法的运算定律:
向量加法的运算定律:
例:在四边形中,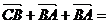
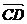
解: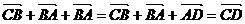
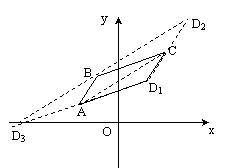 解:当平行四边形为ABCD时,
解:当平行四边形为ABCD时,
仿例三得:D1=(2, 2)
当平行四边形为ACDB时,
仿例三得:D2=(4, 6)
当平行四边形为DACB时,
仿上得:D3=(-6, 0)
求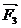 的坐标。
的坐标。
解:由题设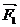 +
+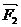 +
+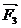 =
=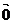 得:(3, 4)+
(2, -5)+(x, y)=(0, 0)
得:(3, 4)+
(2, -5)+(x, y)=(0, 0)
即: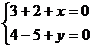 ∴
∴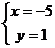 ∴
∴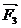 (-5,1)
(-5,1)
4.实数与向量积的坐标运算:已知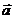 =(x, y) 实数λ
=(x, y) 实数λ
则λ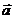 =λ(x
=λ(x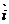 +y
+y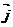 )=λx
)=λx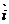 +λy
+λy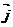
∴λ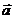 =(λx, λy)
=(λx, λy)
结论:实数与向量的积的坐标,等于用这个实数乘原来的向量相应的坐标。
3.结论:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。
同理可得:一个向量的坐标等于表示此向量的有向线段终点的坐标减去始点的坐标。
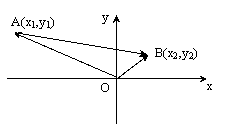
用减法法则:
∵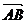 =
= -
-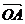 =( x2, y2)
- (x1, y1)
=( x2, y2)
- (x1, y1)
= (x2- x1, y2- y1)
2.解: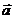 +
+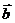 =(x1
=(x1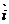 +y1
+y1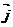 )+( x2
)+( x2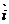 +y2
+y2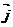 )=(x1+ x2)
)=(x1+ x2) 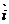 + (y1+y2)
+ (y1+y2) 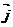
即: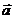 +
+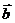 =(x1+ x2, y1+y2)
=(x1+ x2, y1+y2)
同理: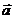 -
-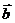 =(x1- x2,
y1-y2)
=(x1- x2,
y1-y2)
1.问题:1°已知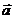 (x1, y1)
(x1, y1) 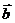 (x2, y2) 求
(x2, y2) 求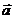 +
+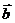 ,
,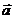 -
-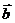 的坐标
的坐标
2°已知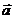 (x, y)和实数λ, 求λ
(x, y)和实数λ, 求λ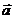 的坐标
的坐标
3.例一:(P109)略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com