解：=

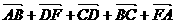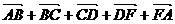
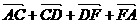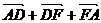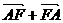　　　　　 ==== 0

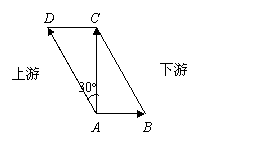例二、在静水中划船的速度是每分钟40，水流的速度是每分钟20，如果船从岸边出发，径直沿垂直与水流的航线到达对岸，那么船行进的方向应该指向何处？

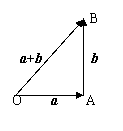
　 解：如图：船航行的方向是

　　　 与河岸垂直方向成30°夹角，

　　　 即指向河的上游。

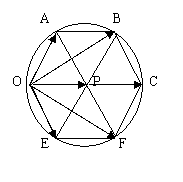
　　　　　　　 向量a、b将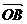、、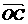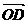表示出来。

　 解：设正六边形中心为P

　　　 则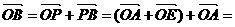a + b + a

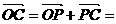　　　　　 　a + b + a + b

　　 由对称性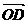：= b + b + a

3．处理《教学与测试》P139-140　 第66课　　 (略)

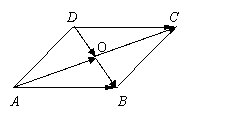　 证：由向量加法法则：

　　 　= +,　 = +

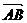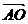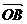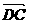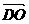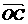
　　　 由已知：=,　 =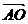

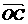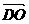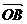
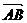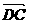　　　 ∴=　　 即AB与CD平行且相等

　　　 ∴ABCD为平行四边形

　　　 则a + b表示向东北走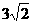km

　 解：= +

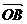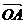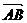
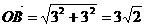　　　 (km)

2．处理《教学与测试》P137-138　 第65课

1°向量的概念：定义、表示法、模、零向量、单位向量、平行向量、

　　　　　　　 相等向量、共线向量

　　 2°向量的加法与减法：定义、三角形法则、平行四边形法则、运算定律

　　　　　 2°交换律和结合律

　　　　　 3°注意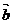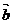：|+| > || + ||不一定成立，因为共线向量不然。

5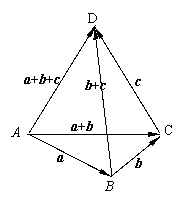．向量加法的结合律：(+) +=+ (+)

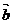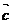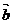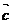证：如图：使, ,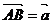

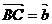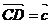
则(+) +=

　 + (+) =

∴(+) +=+ (+)

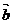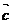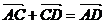
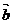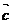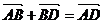
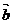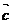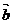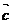从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行。

　　　　 注意：；两个向量的和仍旧是向量(简称和向量)

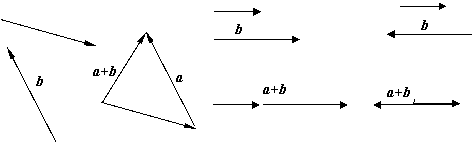
　　　　 强调：

　　　　 1°“向量平移”(自由向量)：使前一个向量的终点为后一个向量的起点

　　　　 2°可以推广到n个向量连加

　　　　 3°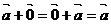

　　　　 4°不共线向量都可以采用这种法则--三角形法则

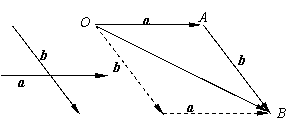　　　 3．例一、已知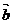向量、，求作向量+

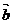
　　　　 作法：在平面内取一点，

　　　　　　　 作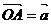

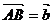
　　　　　　　 则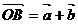

4．加法的交换律和平行四边形法则

　 上题中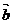+的结果与+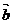是否相同　　 验证结果相同

　 从而得到：1°向量加法的平行四边形法则

　　　　　　 2°向量加法的交换律：+=+

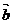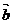4．船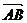速为，水速为，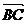

　 则两速度和：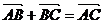

提出课题：向量的加法