
题目列表(包括答案和解析)
2.已知数列1,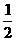 ,
,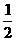 ,
,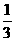 ,
,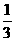 ,
,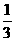 ,
, ,
, ,
, ,
, …,则此数列前100项的和等于()
…,则此数列前100项的和等于()
(A)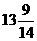 ; (B)
; (B)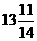 ; (C)
; (C)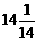 ; (D)
; (D)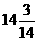
答案:A
1.数列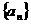 中,
中,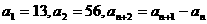 ,
, 等于()
等于()
(A) -56; (B)-43; (C)13; (D)-13
答案:C
19.某企业为筹划资金A 元,以年利率r 每年度利计息借款,在当年初借入,前m 年内不还款,从m+1年度开始每年以一定的金额a 元偿还,但在后续的n 年间要将借款本利和全部还清,求a .
[提示]从借款到还清需m+n 个年份,故A 元的本利和是A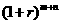 元,而偿还金额的本利和是a
元,而偿还金额的本利和是a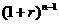 +a
+a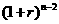 +…+a(1+r)+a=
+…+a(1+r)+a=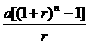
故
A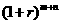 =
=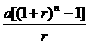 .
.
[答案]a=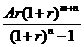 .
.
18.已知函数f(x)=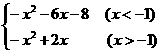
(1)如果当a <-2时,f(-3-a),f(a),-22成等差数列.求a 的值.
(2)在(1)的条件下,设等差数列{an}中,a1=f 2(a),公差为d,并且在前n 项和Sn(n 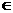 N)中,S2000 最大.求公差d
的取值范围.
N)中,S2000 最大.求公差d
的取值范围.
[提示](1)由a <-2,知-3-a>-1,∴ f(-3-a)=-a2-8 a-15.f(a)=-a2-6 a-8,由已知条件,可得2 f(a)=f(-3-a)-22即有a2+4 a-21=0,∴ a=-7.
(2)a1=f 2(-7)=225,∴ an=225+(n-1)d .
而S2000最大
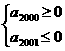

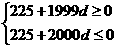
故-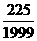 ≤d≤-
≤d≤-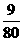 .
.
[答案](1)a=-7.(2)-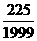 ≤d≤-
≤d≤-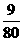 .
.
17.已知等差数列为{an}中,a1=1,S10=100
(1)求数列{an}的通项公式;
(2)从数列{an}中依次取出第1,3,32,…,3n-1 项,组成数列{bn},求数列{bn}的前n 项和.
[提示](1)an=2 n-1.
(2)由于1,3,32,…,3n-1 都是数列{an}中的项,所以它们都满足an=2 n-1故bn=2×3n-1-1.以下再对等比数列{2×3n-1}及常数列1,1,…,分别求其前n 项和即可.
[答案](1)an=2 n-1; (2)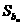 =3n-n-1.
=3n-n-1.
16.已知数列{bn},bn=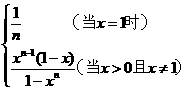
试判断数列{bn}的增减性.
[提示]当x=1时,bn=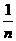 是递减数列;
是递减数列;
当x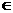 (0,1)时,bn=
(0,1)时,bn=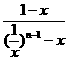 ,∵
,∵ 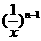 递增,∴ bn 递减.
递增,∴ bn 递减.
当x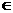 (1,+∞)时,bn=
(1,+∞)时,bn=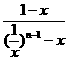 ,∵
,∵ 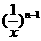 递减且1-x<0,∴ bn 递减.
递减且1-x<0,∴ bn 递减.
总之,数列{bn}是单调递减数列.
15.已知(b-c)log m x+(c-a)log m y+(a-b)log m z=0.
(1)设a、b、c 成等差数列,且公差不为0,求证:x、y、z 成等比数列.
(2)设x、y、z 成等比数列,且公比不为1,求证:a、b、c 成等差数列.
[提示](1)由已知b-c=a-b=-d,c-a=2 d(d ≠0)代入已知等式,得log m x+log m z=2 log m y,故y2=xz .
(2)设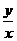 =
=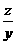 =q(q ≠1),则log m y-log m x=log m z-log m y=log m q ≠0.代入已知等式,得a-2 b+c=0.
=q(q ≠1),则log m y-log m x=log m z-log m y=log m q ≠0.代入已知等式,得a-2 b+c=0.
14.若1+3+5+…+(2 n-1)=110[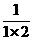 +
+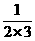 +…+
+…+ ],则n=_____________.
],则n=_____________.
[提示]右式=110[(1-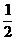 )+(
)+(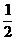 -
-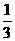 )+…+(
)+…+(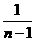 -
-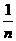 )+(
)+(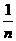 -
-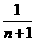 )]
)]
=110(1-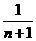 ),
),
左式=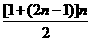 =n2 .
=n2 .
[答案]n=10.
13.已知数列{an}满足a1+2 a2+3 a3+…+nan=n(n+1)(n+2).则它的前n 项和Sn=_______________________.
[提示]∵ a1+2 a2+…+nan=n(n+1)(n+2) ①
∴ a1+2 a2+…+(n-1)an-1=(n-1)n(n+1) ②
由①-②得nan=3 n(n+1),即an=3 n+3
可见,{an}是a1=6,d=3的等差数列.
[答案]Sn=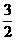 (n2+3 n).
(n2+3 n).
12.等差数列{an}中,S6=0(d ≠0).若am、am+1、a2 m 成等比数列,则m=__________.
[提示]由S6=0推出a1=-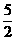 d,又(am+d)2=am(am+md),故可推出2 m2-11 m+12=0.
d,又(am+d)2=am(am+md),故可推出2 m2-11 m+12=0.
[答案]m=4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com