3．已知f(x)＝2 | x|+3，g(x)＝4 x－5，若f 　[p(x)]＝g(x)，则p(3)的值为(　 )．

(A)2　　 (B)±2　　 (C)－2　　 (D)不能确定

[答案](B)．

[点评]本题考察函数概念的对应法则，由已知：2 | p(x)|+3＝4 x－5，所以| p(x)|＝2 x－4，∴　 | p(3)|＝2，故 p(3)＝±2．

2．已知函数f(x)＝a ^x+b 的图象经过点(1，7)其反函数f ^－1(x)的图象经过点(4，0)，则f(x)的表达式是(　 )．

(A)f(x)＝3 ^x+4　　 (B)f(x)＝4 ^x+3

(C)f(x)＝2 ^x+5　　 (D)f(x)＝5 ^x+2

[答案](B)．

[点评]运用f(x)和f ^－1 (x)的关系，f ^－1 (x)的图象经过(4，0)点，可知原来的函数f(x)必过点(0，4)．

1．已知函数f(x)的定义域为[a，b ]且b ＞－a ＞0，则函数F(x)＝f ( x)+f (－x)的定义域是(　 )．

(A)[a，－a ]　　 (B)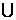(－∞，－a)[a，+∞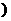

(C)[－a，a ]　　 (D)(－∞，a)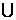[－a，+∞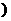

[答案](A)．

[点评]本题考查函数定义域的概念，F (x) 的定义域应满足a ≤x≤b，且a ≤－x≤b，

即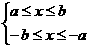解答本题应正确在数轴上画出所示区域，借肋图形得到答案．

20．用若干台拖拉机耕地，若同时投入工作，耕完一片地需要24小时，但它们是每隔相等时间顺序投入工作，每一台投入工作后都工作到耕完为止，如果第一台拖拉机工作时间是最末一台工作时间的5倍，求用这种方法耕完这片土地需要的时间．

[提示]由题设知，每台拖拉机每小时的工作量是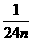．设第一台工作时数为a₁ 小时，第二台工作时数为a₂ 小时，…，最末一台工作时数为a_n 小时，则有

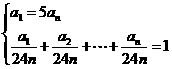，解得a₁＝40．

[答案]40小时．

19．在33和25中间插入两个数，使前三个数成等差数列，后三个数成等比数列．求这两个数．

[提示]设此二数为33+d，33+2 d，则(33+2 d)²＝25(33+d)．解得d₁＝－24，d₂＝

－．

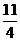[答案]此二数为9，－15或，．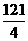

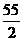18．设等比数列{a_n}的前n 项和为S_n，若S₃+S₆＝2 S₉ ．求数列的公比q ．

[提示]由条件可得关于q 的方程2 q⁶－q³－1＝0．

[答案]q＝－．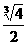

17．已知数列{a_n}是等差数列，数列{b_n}的通项为b_n＝(a₁+a₂+…+a_n)，(n＝1，2，…)求证：数列b_n 也是等差数列．

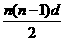[提示]b_n＝[na₁+]＝a₁+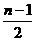·d，再证明b_n+1－b_n＝常数．

16．已知等差数列{a_n}的公差d ≠0，且a₁、a₃、a₉ 成等比数列，则＝___________．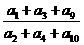

[提示]由已知推出a₁＝d(d ≠0)，并代入所求式中，消去d 即可．

[答案]．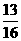

15．已知数列{a_n}中，a₁＝－60，a_n+1＝a_n+3，那么|a₁|+|a₂|+…+|a₃₀|＝_____________．

[提示]令a_n＝－60+(n－1)×3≤0，得n≤21．所以|a₁|+|a₂|+…+|a₃₀|＝－a₁－a₂－…－a₂₁+a₂₂+a₂₃+…+a₃₀，再求S₂₁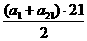＝，a₂₂+…+a₃₀＝．

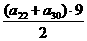[答案]765．

14．等差数列{a_n}的公差d＞0．已知S₆＝51，a₂·a₅＝52．则S₇＝_______________．

[提示]列出a₁ 和d 的方程组，求a₁ 和d ．进而求S₇ ．或由S₆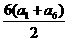＝＝3(a₂+a₅)＝51，得方程组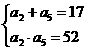，求出a₂，a₅，进而求S₇ ．

[答案]70．