
题目列表(包括答案和解析)
8.设函数f(x)= ,函数g(x)与y=f -1(x+1)的图象关于直线y=x对称,那么g(3)=_______.
,函数g(x)与y=f -1(x+1)的图象关于直线y=x对称,那么g(3)=_______.
[略解]x=f -1 ( y )=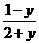 ,x=g-1 (y)=f -1 (y+1)=
,x=g-1 (y)=f -1 (y+1)=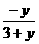 ,y=g(x)=
,y=g(x)=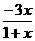 ,
,
故g(3)= .
.
7.若函数f (x)=25-| x+1 |-4×5-| x+1 |-m 的图象与x轴有交点,则实数m 的取值范围是_____.
[略解]f(x)可看作关于5-| x+1 |=t 的二次函数(t ≤1)t 2 -4 t-m,为使它的图象与x轴有交点,只须Dt ≥0,而Dt=16+4 m ≥0,故m的取值范围是m ≥-4.
6.已知二次函数f(x)=ax2+bx,且f(x1)=f(x2)(x1≠x2),则f(x1+x2)=_____.
[略解]由f(x1)=f(x2),将a(x1+x2)(x1-x2)+b(x1-x2)=0
∵ x1 ≠x2,
∴ a(x1+x2)+b=0.
∴ f(x1+x2)= f(-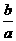 )=
)=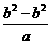 =0.
=0.
5.对于函数f(x)=loga x(其中a >0,a ≠1),若f(3)-f(2)=1,则
f(3.75)+f(0.9)的值等于_________.
[略解]由f(3)-f(2)=loga3-loga 2=loga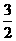 =1,∴ a=
=1,∴ a=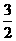 .
.
∴ f(3.75)+f(0.9)=log a3.75×0.9=log a3.375=loga1.53=3 loga 1.5=3.
4.已知函数f(x)=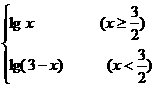 ,若方程f(x)=k 无实根,则实数k 的取值范围是________.
,若方程f(x)=k 无实根,则实数k 的取值范围是________.
[略解]函数f(x)的图象如下图所示,方程f(x)=k 的根,即f(x)的图象与直线g=k 交点的横坐标,由图可见,当k <lg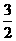 时,f(x)的图象与直线y=k无交点,即方程f(x)=k 无实根,故k 的取值范围是(-∞,lg
时,f(x)的图象与直线y=k无交点,即方程f(x)=k 无实根,故k 的取值范围是(-∞,lg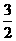 ).
).
3.解方程
(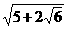 ) x+(
) x+(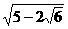 ) x=10.
) x=10.
[略解] ∵ 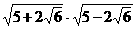 =1,
=1,
∴ 原方程可以改写为:(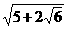 ) x+(
) x+(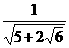 ) x=10,
) x=10,
设y= (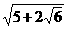 ) x,则y+
) x,则y+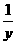 =10,解得y=5±2
=10,解得y=5±2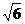 ,
,
于是由(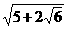 ) x=5±2
) x=5±2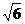 ,得x=±2,
,得x=±2,
∴ 原方程的解为:x=±2.
[点评]
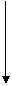 本题的关键是注意到
本题的关键是注意到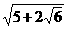 和
和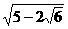 互为倒数,利用整体换元的思想使问题易于解决.
互为倒数,利用整体换元的思想使问题易于解决.
2.当k ∈(0, )时,函数y=
)时,函数y=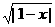 的图象与函数y=kx的图象有多少个不同的交点?
的图象与函数y=kx的图象有多少个不同的交点?
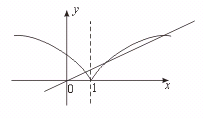
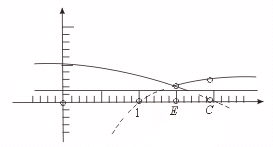
[略解]先作出函数y=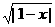 的图象.
的图象.
.
函数y=kx,k ∈(0, )的图象是一条直线,两个函数的图象只可能在第一象限内相交.
)的图象是一条直线,两个函数的图象只可能在第一象限内相交.
当直线y=kx,k ∈(0, )与函数y=
)与函数y=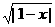 在x>1上的部分相切时,方程
在x>1上的部分相切时,方程
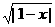 =kx应有重根,即二次方程的判别式为0,D=1-4 k2=0,得k=
=kx应有重根,即二次方程的判别式为0,D=1-4 k2=0,得k= .
.
所以,当0<k < 时,两个图象在x>1时相交于两个点.
时,两个图象在x>1时相交于两个点.
故两个函数的图象有3个交点.
[点评]本题充分体现了数形结合的数学思想方法.在利用图象解题时,要注意用代数的方法解决相交和相切时的数量关系.
1.求函数y= 的定义域.
的定义域.
[略解]x的取值范围,应满足
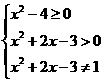
 x<-3且x≠-1-
x<-3且x≠-1-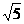 .
.
[点评]
函数的定义域是函数的基本性质之一,应掌握求函数定义域的方法,实际上就是解x所满足的不等式组.
4.(本题满分13分)
已知函数f(x)的定义域为全体实数,且对任意x1,x2∈R有
f (x1)+f (x2)=2 f(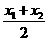 )f(
)f(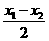 )
)
成立,又知f(a)=0(a ≠0,a 为常数),但f(x)不恒等于0,求证:
(1)f(x)是周期函数,并求出它的一个周期;
(2)f(x)是偶函数;
(3)对任意x∈R,有f(2 x)=2 f 2(x)-1成立.
[略解](1)令x1=x+2 a,x2=x,由已知可得:
f(x+2 a)+f(x)=2 f(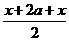 )f(
)f(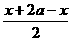 )=2 f(x+a)·f(a)=0,
)=2 f(x+a)·f(a)=0,
∴ f(x+2 a)=-f(x),从而f(x+4 a)=-f(x+2 a)=f(x).
∴ 4 a是f(x)的一个周期.
(2)令x1=x,x2=-x,
则f(x)+f(-x)=2 f(0)f(x)
再令x1=x2=x,则
f(x)+f(x)=2 f(x)f(0).
∴ f(x)+f(-x)=f(x)+f(x).
即 f(-x)=f(x).∴ f(x)是偶函数.
(3)由2 f(x)=2 f(x)f(0)且f(x)≠0,知f(0)=1.
令x1=2 x,x2=0,则有f(2 x)+f(0)=2 f(x)f(x),
即 f(2 x)=2 f 2(x)-1得证.
[点评]若函数f(x)对定义域内任意x满足f(x+T)=f(x)(T是一个不为零的常数),则f(x)是以T为周期的函数.有关周期函数的概念在本章教材中还没有涉及到.
3.(本题满分13分)
已知a ∈N,关于x的方程lg(4-2 x2)=lg(a-x)+1有实根,求a及方程的实根.
[略解] 由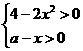 解得-
解得-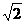 <x<
<x<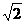 且x<a,
且x<a,
又 方程4-2 x2=10(a-x),
整理得:x2-5 x+5 a -2=0,D=25-4(5 a -2)≥0,
得a ≤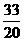 ,
,
又 a ∈N,∴ a=1.
此时方程化为:x2-5 x+3=0,
∴ x=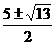 ;
;
又
-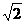 <x<1,∴ x=
<x<1,∴ x=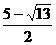 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com