
题目列表(包括答案和解析)
2.已知函数y=2 x2+4 (a -4) x+5,在(-∞,-3)上是减函数,则a 的取值范围是________.
[答案]a ≤7.
[点评]要切实掌握好二次函数的定义及有关的性质,本题中函数图象对称轴方程是x=4-a,且开口向上,故只要4-a ≥-3即可.
1.若(x,y)在一一映射下的象是(x+y,x-y),其中x∈R,y ∈R,则(1,2)的象是_________;(1,-3)的原象是___________.
[答案](3,-1);(-1,2).
6.函数f(x)=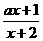 在区间(-2,+∞)上是增函数,那么a 的取值范围是( ).
在区间(-2,+∞)上是增函数,那么a 的取值范围是( ).
(A)0<a <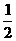 (B)a >
(B)a >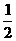
(C)a <-1或a >1 (D)a >-2
[答案](B).
[点评]利用反比例函数的单调性,函数y=a+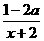 即(x+2)(y -a)=1-2 a .若在(-2,+∞)上是增函数,只需1-2 a <0,故a >
即(x+2)(y -a)=1-2 a .若在(-2,+∞)上是增函数,只需1-2 a <0,故a >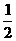 .
.
5.将函数y=f(x-1)的图象作适当的平移,可得到函数y=f(x+2)的图象,这个平移是( ).
(A)向左平移3个单位 (B)向右平移3个单位
(C)向左平移2个单位 (D)向右平移2个单位
[答案](A).
[点评]函数y=f(x+a)(a >0)的图象是由y=f(x)向左平移a个单位得到的.将y=f(x-1)的图象向左平移3个单位,就得到y=f(x+3-1)=f(x+2)的图象.
4.若loga2 <logb2 <0,则( ).
(A)0<a <b <1 (B)0<b <a <1
(C)a >b >1 (D)b >a >1
[答案](B).
[点评]利用对数函数的图象和性质以及换底公式可解.
[提示]loga 2=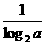 ,logb 2=
,logb 2=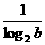 ,
,
由 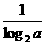 <
<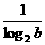 <0,
<0,
得 0>log2 a >log2 b,
∴ 1>a >b >0.
3.设a=0.32,b=log20.3,c=20.3,这三个函数之间的大小关系是( ).
(A)a <c <b (B)a <b <c
(C)b <a <c (D)b <c <a
[答案](C).
[点评]三个数中a >0,c >0,b <0,否定(A),(B).而a <1,c>1,故选(C).
2.设f(x)=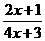 (x∈R且x≠-
(x∈R且x≠-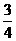 ),则f -1 (2)等于( ).
),则f -1 (2)等于( ).
(A)-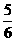 (B)
(B)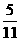
(C) (D)-
(D)-
[答案](A).
[点评]运用反函数的概念,只需在原函数中令2=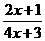 ,解出x,即为所求.
,解出x,即为所求.
1.下列各函数中,图象完全相同的是( ).
(A)y=2 lg x和y=lg x2
(B)y=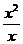 和 y=x
和 y=x
(C)y=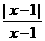 和y=
和y=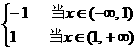
(D)y=x-3和y=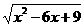
[答案](C).
[点评]应考察每组两个函数的定义域和对应法则是否相同.
10.设f(x)=3 x-2 f( ),x≠0.求f(x).
),x≠0.求f(x).
[略解]令y= ,则x=
,则x=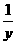 ,代入方程,
,代入方程,
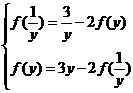 消去
消去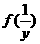 ,得f(y)=
,得f(y)= .
.
故 f(x)=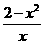 .
.
9.定义在自然数集上的函数f(x),x∈N,f(1)=1,f(m+n)=f(m)+f(n)+m · n,m,n ∈N.求f(x).
[略解]令m=1,代入上式,得f(1+n)=f(1)+f(n)+n=f(n)+(n+1),
即 f(n+1)-f(n)=n+1.
取n=1,2,3,…,x-1,得
f(2)-f(1)=2
f(3)-f(2)=3
……
f(x)-f(x-1)=x+1.
以上各式相加,得f(x)-f(1)=2+3+…+(x+1).
∴ f(x)=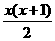 (x∈N).
(x∈N).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com