
题目列表(包括答案和解析)
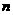 的值。
的值。
(1)
设集合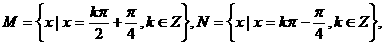 则
则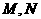 之间的关系为_______。
之间的关系为_______。
(2)
半径是 ,圆心角是
,圆心角是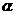 (弧度)的扇形的面积为_______。
(弧度)的扇形的面积为_______。
(3)
函数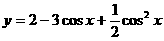 的最小值为_______。
的最小值为_______。
(4)
函数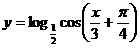 在区间_______上是减函数。
在区间_______上是减函数。
(5)
已知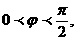 且
且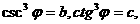 那么
那么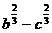 的值为_______。
的值为_______。
(1)设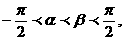 则
则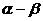 的范围是( )
的范围是( )
(A) (B)
(B)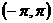
(C)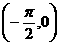 (D)
(D)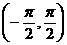
(2)设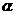 是第二象限角,则
是第二象限角,则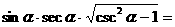 ( )
( )
(A)1
(B)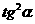 (C)
(C) (D)
(D)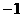
(3)函数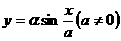 的最小正周期是( )
的最小正周期是( )
(A)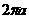 (B)
(B)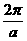 (C)
(C)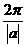 (D)
(D)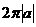
(4)函数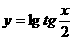 的定义域为( )
的定义域为( )
(A)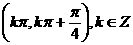 (B)
(B)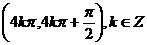
(C)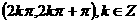 (D)第一、第三象限角所成集合
(D)第一、第三象限角所成集合
(5)函数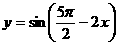 ( )
( )
(A)是奇函数 (B)是偶函数
(C)既不是奇函数,也不是偶函数 (D)奇偶性无法判断
(6)函数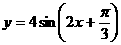 的图象( )
的图象( )
(A)关于直线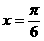 对称
(B)关于直线
对称
(B)关于直线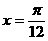 对称
对称
(C)关于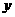 轴对称 (D)关于原点对称
轴对称 (D)关于原点对称
(7)满足不等式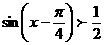 的
的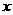 的集合是( )
的集合是( )
(A)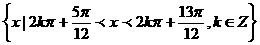
(B)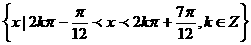
(C)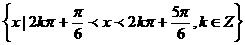
(D)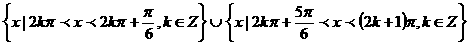
(8)把函数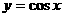 的图象上所有的点的横坐标缩小到原来的一半,纵坐标保持不变,然后把图象向左平移
的图象上所有的点的横坐标缩小到原来的一半,纵坐标保持不变,然后把图象向左平移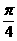 个单位长度,得到新的函数图象,那么这个新函数的解析式为( )
个单位长度,得到新的函数图象,那么这个新函数的解析式为( )
(A)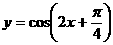 (B)
(B)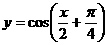
(C)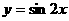 (D)
(D)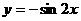
(9)已知实数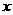 满足关系式
满足关系式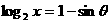 ,那么
,那么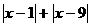 的值是( )
的值是( )
(A)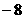 (2)8
(3)
(2)8
(3)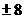 (D)与
(D)与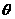 的取值有关
的取值有关
(10)已知圆柱的底面半径长为R,上底半径OB与下底半径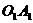 所成的角为
所成的角为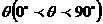 ,那么圆柱的轴
,那么圆柱的轴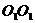 与
与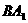 且垂直于底面的平面的距离为( )
且垂直于底面的平面的距离为( )
(A) (B)
(B)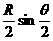 (C)
(C)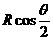 (D)
(D)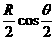
8.(1)f(x)=[x-(n+1)2]+3n-8 ∴an=3n-8,∵ an+1-an=3 , ∴{an}为等差数列。
(2)b0=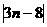
当1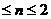 时,bn=8-3n,b1=5。Sn=
时,bn=8-3n,b1=5。Sn=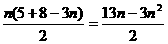
当n 3时。bn=3n-8 Sn=5+2+1+4+…(3n-8)
3时。bn=3n-8 Sn=5+2+1+4+…(3n-8)
=7+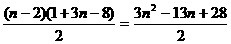
∴Sn=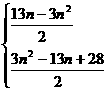
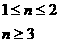
7.由S20=S10得2a1+29d=0 d=-2,an=a1+(n-1)d=-2n+31
d=-2,an=a1+(n-1)d=-2n+31
Sn=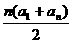 =-n2+30n=-(n-15)2+225 ∴当n=15时,Sn最大,最大值为225。
=-n2+30n=-(n-15)2+225 ∴当n=15时,Sn最大,最大值为225。
6.购买时付了150元,欠款1000元。每月付50元,分20次付完,设每月付款数顺次组成数列{an},则
a1=50+1000×0.01=60
a2=50+(1000-50) ×0.01=60-0.5
a3=50+(1000-50×2) ×0.01=60-0.5×2
类推,得
a10=60-0.5×9=55.5
an=60-0.5(n-1)(1 n
n 20)。
20)。
∴ 付款数{an}组成等差数列,公差d=-0.5,全部贷款付清后,付款总数为
S20+150=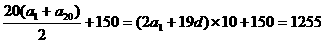 (元)。
(元)。
5.设S表示从1到100的所有整数之和。S1表示从1到100中所在能被3整除的整数的和。
S2表示从1到100中所有能被5整除的整数的和。
S3表示从1到100中所有既能被3整除,又能被5整除的整数的和。
则S=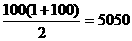 。
。
由99=3+(n-1)×3,得n=33。 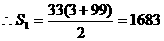 。
。
由100=5+(n-1) ×5,得n=20。 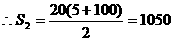
S3表示15,30,45,…,90之和 S3=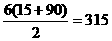
从1到100中所有不被3及5整除的整数之和为S-S1-S2+S3=2632。
4.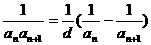
∴Sn=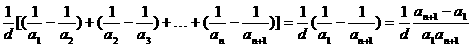
=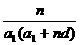 。
。
3.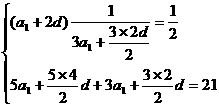
 由①,得a1=d。由②,得8a1+13d=1。
由①,得a1=d。由②,得8a1+13d=1。
故a1=d=1。
∴Sn=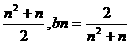
2.当n=1时,a1=S1=1+c
当n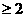 时,an=Sn-Sn-1=(n2+c)-[(n2+c)]-[(n-1)2+C]=2n-1。
时,an=Sn-Sn-1=(n2+c)-[(n2+c)]-[(n-1)2+C]=2n-1。
∴an=
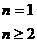
若C=0,an=2n-1,此时an-an-1=2(n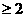 ){an}为等差数列。
){an}为等差数列。
若C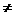 0,C+1
0,C+1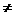 1,{an}不为等差数列。
1,{an}不为等差数列。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com