
题目列表(包括答案和解析)
5.设有两个命题①关于x的不等式x2+2ax+4>0对于一切x∈R恒成立,②函数f(x)=-(5-2a)x是减函数,若此二命题有且只有一个为真命题,则实数a的范围是( )
A.(-2,2) B.(-∞,2) C.(-∞,-2) D.(-∞,-2]
考查二次函数性质及逻辑推理能力.
[解析] ①等价于Δ=(2a)2-16<0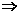 -2<a<2
-2<a<2
②等价于5-2a>1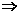 a<2
a<2
①②有且只有一个为真,∴a∈(-∞,-2]
[答案] D
4.设x∈R,若a<lg(|x-3|+|x+7|)恒成立,则( )
A.a≥1 B.a>1 C.0<a≤1 D.a<1
考查对数函数性质及绝对值不等式.
[解析] 令t=|x-3|+|x+7|,∴x∈R,∴tmin=10
y=lgt≥lg10=1,故a<1
[答案] D
3.若a>1,b>1,且lg(a+b)=lga+lgb,则lg(a-1)+lg(b-1)的值等于( )
A.0 B.lg2 C.1 D.-1
考查对数运算.
[解析] 由lg(a+b)=lga+lgb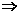 a+b=ab
a+b=ab
即(a-1)(b-1)=1,∴lg(a-1)+lg(b-1)=0
[答案] A
2.函数y=log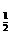 (x2-6x+17)的值域是( )
(x2-6x+17)的值域是( )
A.R B.[8,+ C.(-∞,-
C.(-∞,-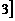 D.[-3,+∞)
D.[-3,+∞)
考查对数函数单调性、定义域、值域.
[解析] y=log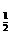 [(x-3)2+8]≤log
[(x-3)2+8]≤log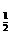 8=-3
8=-3
[答案] C
1.已知2lg(x-2y)=lgx+lgy,则 的值为( )
的值为( )
A.1 B.4 C.1或4 D.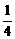 或4
或4
考查对数函数及对数函数定义域.
[解析] 原命题等价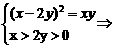 x=4y
x=4y
∴ =4
=4
[答案] B
高中代数“两角和与差的三角函数、解斜三角形”检查题
 求复合振动
求复合振动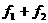 的振幅、周期和初相。
的振幅、周期和初相。
(1)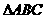 中,
中,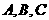 分别为
分别为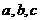 三条边的对角,如果
三条边的对角,如果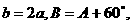 那么
那么
(2)已知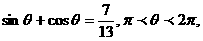 那么
那么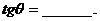
(3)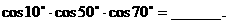
(1)已知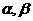 均属于
均属于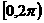 ,且有以下三个命题:
,且有以下三个命题:
①如果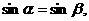 那么
那么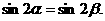
②如果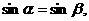 那么
那么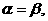 或
或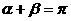
③如果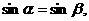 那么
那么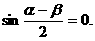
上述命题中,真命题的个数是( )
(A)0 (B)1 (C)2 (D)3
(2)在下列函数中,以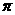 为最小正周期,且在
为最小正周期,且在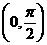 内是增函数的是( )
内是增函数的是( )
(A)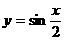 (B)
(B)
(C)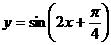 (D)
(D)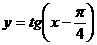
(3)等式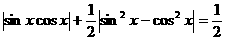 成立的充要条件是
成立的充要条件是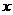 等于( )
等于( )
(A)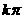 (B)
(B)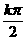 (C)
(C)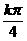 (D)
(D)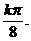 其中
其中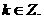
(4)已知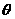 是第二象限的角,且满足
是第二象限的角,且满足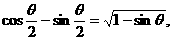 那么
那么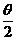 ( )
( )
(A)是第一象限角 (B)是第二象限角
(C)是第三象限角 (D)可能是第一象限角,也可能是第三象限角
(5)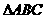 中,
中,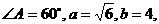 那么满足条件的
那么满足条件的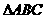 ( )
( )
(A)无解 (B)有1个解
(C)有2个解 (D)不能确定
(6)已知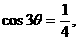 那么
那么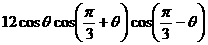 的值是( )
的值是( )
(A)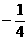 (B)
(B)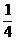
(C) (D)
(D)
(7)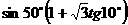 的值是( )
的值是( )
(A)1
(B)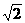 (3)
(3)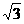 (4)2
(4)2
(8)函数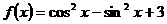 的图象的一条对称轴的方程是( )
的图象的一条对称轴的方程是( )
(A)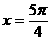 (B)
(B)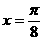 (C)
(C)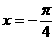 (D)
(D)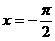
已知函数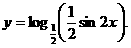
(1) 求它的定义域、值域以及在什么区间上是增函数;
(2) 判断它的奇偶性;
(3) 判断它的周期性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com