
题目列表(包括答案和解析)
16.(本小题满分10分)已知y=log4(2x+3-x2).
(1)求定义域;
(2)求f(x)的单调区间;
(3)求y的最大值,并求取最大值时x值.
考查对数函数、二次函数的单调性、最值.
[解] (1)由2x+3-x2>0,解得-1<x<3
∴f(x)定义域为{x|-1<x<3}
(2)令u=2x+3-x2,则u>0,y=log4u
由于u=2x+3-x2=-(x-1)2+4
再考虑定义域可知,其增区间是(-1,1),减区间是[1,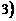
又y=log4u为(0,+∞)增函数,
故该函数单调递增区间为?(-1,?1],减区间为[1,3)
(3)∵u=2x+3-x2=-(x-1)2+4≤4
∴y=log4u≤log44=1
故当x=1时,u取最大值4时,y取最大值1.
15.(本小题满分8分)已知函数f(x)=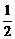 +lg
+lg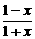 .
.
(1)求此函数的定义域,并判断函数单调性.
(2)解关于x的不等式f[x(x-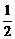 )]<
)]<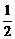 .
.
[解] (1)f(x)=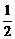 +lg
+lg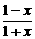 =
=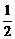 +lg(-1+
+lg(-1+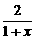 )
)
要使f(x)有意义,即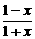 >0,∴f(x)的定义域为-1<x<1
>0,∴f(x)的定义域为-1<x<1
设-1<x1<x2<1,则f(x1)-f(x2)=lg(-1+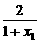 )-lg(-1+
)-lg(-1+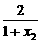 )
)
∵-1<x1<x2<1,∴0<x1+1<x2+1
∴-1+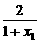 >-1+
>-1+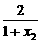
∴f(x1)>f(x2),即f(x)在(-1,1)上为减函数
(2)∵f(0)=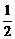 ,∴f[x(x-
,∴f[x(x-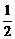 )]<
)]<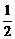 =f(0)
=f(0)
由(1)知f(x)在(-1,1)上为奇函数
∴ ,解得:
,解得: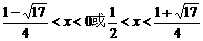
即不等式解集为(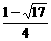 ,0)∪(
,0)∪(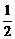 ,
,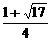 )
)
14.国家规定的个人稿酬纳税方法是:不超过800元的不纳税,超过800元而不超过4000元的按超过800元的14%纳税;超过4000元按全部稿酬的11%纳税,某人出版了一本书,共纳税420元,他的稿费为______元.
考查函数应用及解决实际问题的能力.
[解析] 若其稿费为4000,则应纳税3200×14%=448>420
故稿费应小于4000元,设为x元
则(x-800)14%=420,解得x=3800(元)
[答案] 3800
13.设函数f(x)=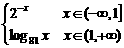 ,则满足f(x)=
,则满足f(x)= 的值为______.
的值为______.
考查分段函数对应法则理解及对数运算.
[解析] 若x∈(-∞,1),有2-x= ,∴x=2,但2
,∴x=2,但2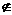 (-∞,
(-∞,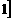 ;
;
若x∈(1,+∞),有log81x=
∴x=3符合题意
[答案] 3
12.函数f(x)=ax(a>0且a≠1)在区间[1,2]上的最大值比最小值大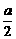 ,则a的值为______.
,则a的值为______.
考查指数函数的单调性及解决问题的能力.
[解析] 当a>1时,f(x)为增函数,a2-a=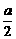 ,得a=
,得a=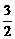
当0<a<1时,f(x)=ax在[1,2]上为减函数,
有a-a2=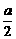
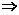 a=
a=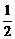 ,
,
故a=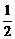 或
或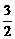
[答案] 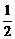 或
或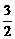
11.方程log3(1-2·3x)=2x+1的解x=______.
考查对数与指数运算.
[解析] 32x+1=1-2·3x,即3(3x)2+2·3x-1=0
解得3x=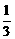 ,故x=-1
,故x=-1
[答案] -1
10.今有一组实验数据如下:
|
t |
1.99 |
3.0 |
4.0 |
5.1 |
6.12 |
|
v |
1.5 |
4.04 |
7.5 |
12 |
18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.v=log2t B.v=log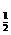 t C.v=
t C.v=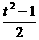 D.v=2t-2
D.v=2t-2
考查构建数学模型的能力,具开放性.
[解析] 五组数据,取近似值1.99≈2;4.04≈4;5.1≈5,18.01≈18,
代入验证可知v=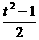 最接近.
最接近.
[答案] C
第Ⅱ卷(非选择题 共70分)
9.若x0是方程2x=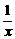 的解,则x0∈( )
的解,则x0∈( )
A.(0.1,0.2) B.(0.3,0.4) C.(0.5,0.7) D.(0.9,1)
考查指数函数图象性质及估算能力.
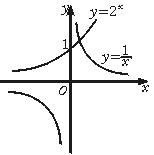 [解析] 画出y=2x,y=
[解析] 画出y=2x,y=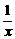 图象.
图象.
∵20.1<20.2<1,而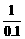 >
> =5
=5
排除A,同理排除B
20.5=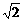 ≈1.414,20.7>20.5,
≈1.414,20.7>20.5,
而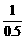 =2,
=2,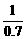 ≈1.428
≈1.428
21>20.9>20.5≈1.414,而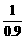 ≈1.11
≈1.11
[答案] C
8.若定义运算a*b=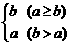 ,则函数f(x)=3x*3-x的值域是( )
,则函数f(x)=3x*3-x的值域是( )
A.(0,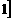 B.[1,+
B.[1,+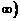 C.(0,+∞) D.(-∞,+∞)
C.(0,+∞) D.(-∞,+∞)
考查函数值域及灵活运用能力.
[解析] 若3x≥3-x,即x≥0,则f(x)=3-x
若3x<3-x,即x<0,则f(x)=3x
故值域为(0,1]
[答案] A
7.若函数y=log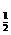 (2-log2x)的值域是(-∞,0),则其定义域是( )
(2-log2x)的值域是(-∞,0),则其定义域是( )
A.x<2 B.0<x<2 C.0<x<4 D.2<x<4
考查对数函数定义域、值域.
[解] 令2-log2x=u,由题意知u>1,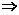 log2x<1,故0<x<2.
log2x<1,故0<x<2.
[答案] B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com