
题目列表(包括答案和解析)
7.函数y=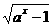 的定义域是(-∞,0],则a的取值范围是__________.
的定义域是(-∞,0],则a的取值范围是__________.
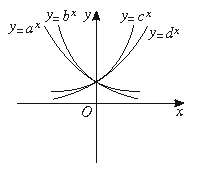
6.在同一坐标系下,函数y=ax,y=bx,y=cx,y=dx的图象如下图,则a、b、c、d、1之间从小到大的顺序是__________.
5.已知函数f(x)=a1-x(a>0,a≠1),当x>1时恒有f(x)<1,则f(x)在R上是
A.增函数
B.减函数
C.非单调函数
D.以上答案均不对
4.下列函数中,值域是(0,+∞)的共有
①y=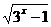 ②y=(
②y=(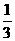 )x
③y=
)x
③y=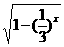 ④y=3
④y=3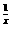
A.1个 B.2个
C.3个 D.4个
3.下列说法中,正确的是
①任取x∈R都有3x>2x ②当a>1时,任取x∈R都有ax>a-x
③y=( )-x是增函数 ④y=2|x|的最小值为1
⑤在同一坐标系中,y=2x与y=2-x的图象对称于y轴
)-x是增函数 ④y=2|x|的最小值为1
⑤在同一坐标系中,y=2x与y=2-x的图象对称于y轴
A.①②④ B.④⑤
C.②③④ D.①⑤
2.集合M={x|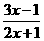 ≥0},N={x|3(3x-1)(2x+1)≥1},则集合M、N的关系是
≥0},N={x|3(3x-1)(2x+1)≥1},则集合M、N的关系是
A.M=N B.M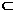 N
N
C.M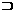 N D.M
N D.M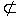 N
N
1.如果函数y=ax(a>0,a≠1)的图象与函数y=bx(b>0,b≠1)的图象关于y轴对称,则有
A.a>b
B.a<b
C.ab=1
D.a与b无确定关系
19.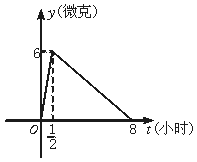 (本小题满分12分)某医药研究所开发一种新药,如果成人按规定的剂量使用,据监测,服药后每毫升血液中的含药量y与时间t之间近似满足如图曲线
(本小题满分12分)某医药研究所开发一种新药,如果成人按规定的剂量使用,据监测,服药后每毫升血液中的含药量y与时间t之间近似满足如图曲线
(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药为7:00,问一天中怎样安排服药时间、次数,效果最佳?
考查函数应用及分析解决问题的能力.
[解] (1)依题意,得y=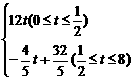
(2)设第二次服药时,在第一次服药后t1小时
则-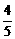 t1+
t1+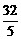 =4,t1=3
=4,t1=3
因而第二次服药应在10:00
设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药后含药量之和,即有-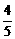 t2+
t2+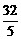 -
-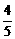 (t2-3)+
(t2-3)+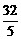 =4
=4
解得:t2=7(小时)
设第四次服药在第一次服药后t3小时(t3>8),则此时第一次服的药已吸收完,此时血液中含药量应为第二、三次之和
-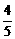 (t3-3)+
(t3-3)+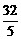 +[-
+[-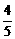 (t3-7)+
(t3-7)+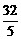 ]=4
]=4
解得t3=10.5小时
故第四次服药应在17:30.
18.(本小题满分12分)若p∈R,且当|log2p|<2时,不等式px+1>2x-p恒成立,试求x的取值范围.
考查对数基本概念及分类讨论思想.
[解] 由|log2p|<2得-2<log2p<2,则 <p<4
<p<4
由不等式px+1>2x-p,得p(x+1)>2x-1
①当x>-1时,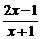 <p,即
<p,即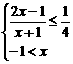 ,解得-1<x≤
,解得-1<x≤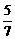
②当x<-1时,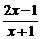 >p,即
>p,即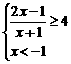 ,解得-
,解得-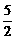 ≤x<-1
≤x<-1
∴x的取值范围为(-1,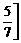 ∪[-
∪[-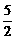 ,-
,-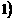
17.(本小题满分12分)已知函数f(x)=2x-x2(x≥0),问是否存在这样的正数a、b,当x∈[a,b]时g(x)=f(x),且g(x)值域[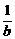 ,
,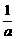 ]?若存在,求出所有a、b之值,若不存在,请说明理由.
]?若存在,求出所有a、b之值,若不存在,请说明理由.
考查函数知识综合运用,分类讨论思想.
[解] 分三种情况讨论:
①当0<a<b≤1时,那么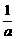 >1,而当x≥0时,f(x)的最大值为1,故此时不可能使g(x)=f(x)
>1,而当x≥0时,f(x)的最大值为1,故此时不可能使g(x)=f(x)
②当0<a<1<b时,则g(x)最大值为g(1)=f(1)=1,
即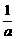 =1,得a=1与0<a<1<b矛盾
=1,得a=1与0<a<1<b矛盾
③当1≤a<b时,∵x≥1,f(x)为减函数,
则g(x)=f(x)=2x-x2,于是有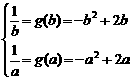
即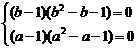
∵1≤a<b,∴a=1,b=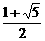
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com