
题目列表(包括答案和解析)
两个有效数字)
解略 见P129 注意由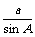 =
=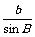 求出sinB=0.8999 B角有两解
求出sinB=0.8999 B角有两解
解略 见P128 注意强调“对”
2.两边和其中一边对角,求另一边的对角,进而可求其它的边和角。
从理论上正弦定理可解决两类问题:
1.两角和任意一边,求其它两边和一角;
4.突出几点:1°正弦定理的叙述:在一个三角形中。各边和它所对角的正弦
比相等,即: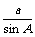 =
=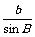 =
=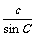 它适合于任何三角形。
它适合于任何三角形。
2°可以证明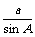 =
=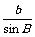 =
=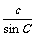 =2R (R为△ABC外接圆半径)
=2R (R为△ABC外接圆半径)
3° 每个等式可视为一个方程:知三求一
sinA=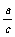 sinB=
sinB=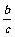 sinC=1 即:
sinC=1 即:
c=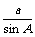 c=
c=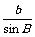 c=
c=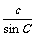 ∴
∴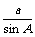 =
=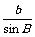 =
=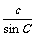
2.能否推广到斜三角形?
证明一(传统证法)在任意斜△ABC当中:
S△ABC=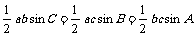
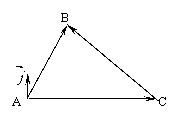 两边同除以
两边同除以 即得:
即得: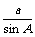 =
=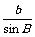 =
=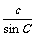
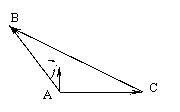 3.用向量证明:
3.用向量证明:
证二:过A作单位向量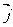 垂直于
垂直于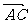
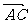 +
+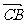 =
=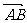 两边同乘以单位向量
两边同乘以单位向量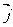
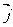 •(
•(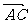 +
+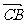 )=
)=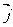 •
•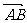
则: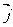 •
•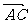 +
+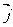 •
•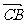 =
=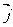 •
•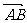
∴|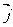 |•|
|•|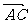 |cos90°+|
|cos90°+|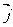 |•|
|•|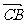 |cos(90°-C)=|
|cos(90°-C)=|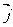 |•|
|•|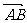 |cos(90°-A)
|cos(90°-A)
∴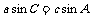 ∴
∴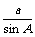 =
=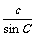
同理:若过C作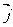 垂直于
垂直于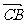 得:
得: 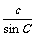 =
=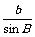 ∴
∴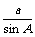 =
=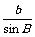 =
=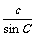
当△ABC为钝角三角形时,设 ÐA>90° 过A作单位向量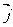 垂直于向量
垂直于向量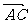
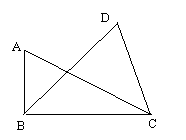 补充:1.在△ABC中,求证:
补充:1.在△ABC中,求证: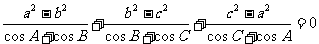
2.如图AB^BC CD=33 ÐACB=30°
ÐBCD=75°
ÐBDC=45° 求AB的长 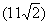
1°求最大角 2°求以此最大角为内角,夹此角两边之和为4的平行四边形的最大面积。
解:1°设三边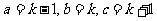
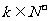 且
且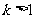
∵C为钝角 ∴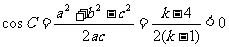 解得
解得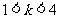
∵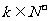 ∴
∴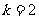 或3 但
或3 但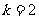 时不能构成三角形应舍去
时不能构成三角形应舍去
当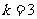 时
时 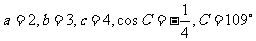
2°设夹C角的两边为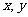
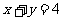
S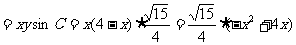
当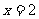 时S最大=
时S最大=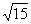
证略 见P159
注意:1.这是正弦定理的又一种证法(现在共用三种方法证明)
2.正弦定理的三种表示方法(P159)
例二 在任一△ABC中求证: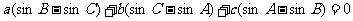
证:左边=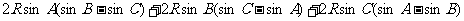 =
=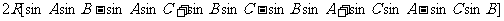 =0=右边
=0=右边
例三 在△ABC中,已知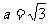 ,
,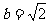 ,B=45° 求A、C及c
,B=45° 求A、C及c
解一:由正弦定理得: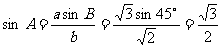
∵B=45°<90° 即b<a ∴A=60°或120°
当A=60°时C=75° 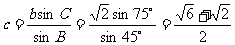
当A=120°时C=15° 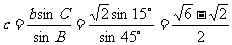
解二:设c=x由余弦定理 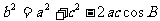
将已知条件代入,整理: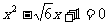
解之:
当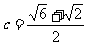 时
时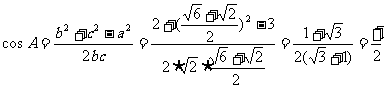
从而A=60° C=75°
当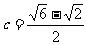 时同理可求得:A=120°
C=15°
时同理可求得:A=120°
C=15°
例四 试用坐标法证明余弦定理
证略见P161
例五 在△ABC中,BC=a, AC=b, a, b是方程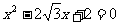 的两个根,且
的两个根,且
2cos(A+B)=1 求 1°角C的度数 2°AB的长度 3°△ABC的面积
解:1°cosC=cos[p-(A+B)]=-cos(A+B)=-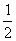 ∴C=120°
∴C=120°
2°由题设: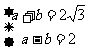
∴AB2=AC2+BC2-2AC•BC•osC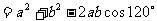
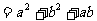
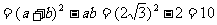 即AB=
即AB=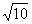
3°S△ABC=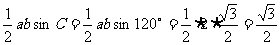
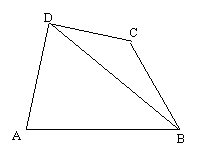 例六 如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长
例六 如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长
解:在△ABD中,设BD=x
则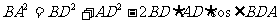
即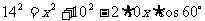
整理得: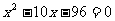
解之: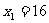
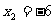 (舍去)
(舍去)
由余弦定理: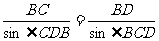 ∴
∴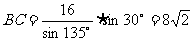
12.已知函数 的定义域为
的定义域为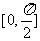 ,值域为[-5,1]。求常a,b的值。
,值域为[-5,1]。求常a,b的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com