5.设S表示从1到100的所有整数之和。S₁表示从1到100中所在能被3整除的整数的和。

S₂表示从1到100中所有能被5整除的整数的和。

S₃表示从1到100中所有既能被3整除，又能被5整除的整数的和。

则S=。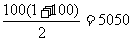

由99=3+(n-1)×3,得n=33。　 。

由100=5+(n-1) ×5,得n=20。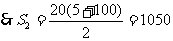　　

S₃表示15，30，45，…，90之和　 S₃=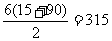

从1到100中所有不被3及5整除的整数之和为S-S₁-S₂+S₃=2632。

4.

∴Sn=

=。

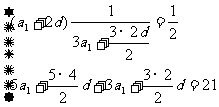
3．　 　由①，得a₁=d。由②，得8a₁+13d=1。

故a₁=d=1。

∴S_n=

2．当n=1时，a₁=S₁=1+c

当n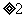时，a_n=S_n-S_n-1=(n²+c)-[(n²+c)]-[(n-1)²+C]=2n-1。

∴a_n=　

若C=0，a_n=2n-1,此时a_n-a_n-1=2(n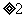){a_n}为等差数列。

若C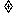0,C+1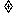1,{a_n}不为等差数列。

1．

S₅₀-S₃₀=a₃₁+a₃₂

+…+a₅₀==30-50=-20。

∴a₁+a₈₀=-2　 ∴S₈₀=。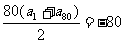

10．。

9．10

a₁+a₂+a₃=12,a_n-2+a_n-1+a_n=132,相加得3(a₁+a_n)=144,a₁+a_n=48,求得S_n==240,n=10。

8．8或9a₁+3d=-(a₁+13d),得a₁=-8d　 由　　 得

1.p+(2n-1)(q-p)　 2.14　 3.72　 4.9　 5.1428　 6.2,5,8,11或11,8,5,2。　 7。。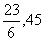

20．四根之和为2，则四根为。

a=得a+b=。