
题目列表(包括答案和解析)
6.下列语句:(1)0与{0}表示同一个集合;(2)由1,2,3组成的集合可表示为{1,2,3}或{3,2,1};(3)方程(x-1)2(x-2)2=0的所有解的集合可表示为{1,1,2};(4)集合{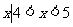 }是有限集,正确的是( )
}是有限集,正确的是( )
(A)只有(1)和(4) (B)只有(2)和(3)
(C)只有(2) (D)以上语句都不对
5.已知集合A={ } B={
} B={ }则A
}则A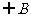 =( )
=( )
(A)R
(B){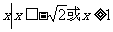 }
}
(C){ } (D){
} (D){ }
}
4.设A、B是全集U的两个子集,且A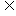 B,则下列式子成立的是( )
B,则下列式子成立的是( )
(A)CUA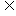 CUB (B)CUA
CUB (B)CUA CUB=U
CUB=U
(C)A CUB=
CUB= (D)CUA
(D)CUA B=
B=
3.集合A={x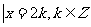 } B={
} B={ } C={
} C={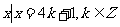 }又
}又 则有( )
则有( )
(A)(a+b) A
(B) (a+b)
A
(B) (a+b)  B
(C)(a+b)
B
(C)(a+b)  C (D) (a+b)
C (D) (a+b)  A、B、C任一个
A、B、C任一个
2.集合{1,2,3}的真子集共有( )
(A)5个 (B)6个 (C)7个 (D)8个
1.下列八个关系式①{0}= ②
② =0 ③
=0 ③ {
{ } ④
} ④
 {
{ } ⑤{0}
} ⑤{0}
 ⑥0
⑥0
 ⑦
⑦
 {0} ⑧
{0} ⑧
 {
{ }其中正确的个数( )
}其中正确的个数( )
(A)4 (B)5 (C)6 (D)7
第一单元 集合
[重点]
理解集合的概念,集合的性质,元素与集合的表示方法及其关系。
集合的子、交、并、补的意义及其运用。掌握有关术语和符号,准确使用集合语言表述、研究、处理相关数学问题。
[难点]
有关集合的各个概念的涵义以及这些概念相互之间的区别与联系。
准确理解、运用较多的新概念、新符号表示处理数学问题。
8.(1)f(x)=[x-(n+1)2]+3n-8 ∴an=3n-8,∵ an+1-an=3 , ∴{an}为等差数列。
(2)b0=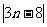
当1 时,bn=8-3n,b1=5。Sn=
时,bn=8-3n,b1=5。Sn=
当n 3时。bn=3n-8 Sn=5+2+1+4+…(3n-8)
3时。bn=3n-8 Sn=5+2+1+4+…(3n-8)
=7+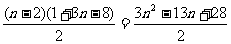
∴Sn=
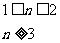
7.由S20=S10得2a1+29d=0 d=-2,an=a1+(n-1)d=-2n+31
d=-2,an=a1+(n-1)d=-2n+31
Sn= =-n2+30n=-(n-15)2+225 ∴当n=15时,Sn最大,最大值为225。
=-n2+30n=-(n-15)2+225 ∴当n=15时,Sn最大,最大值为225。
6.购买时付了150元,欠款1000元。每月付50元,分20次付完,设每月付款数顺次组成数列{an},则
a1=50+1000×0.01=60
a2=50+(1000-50) ×0.01=60-0.5
a3=50+(1000-50×2) ×0.01=60-0.5×2
类推,得
a10=60-0.5×9=55.5
an=60-0.5(n-1)(1 n
n 20)。
20)。
∴ 付款数{an}组成等差数列,公差d=-0.5,全部贷款付清后,付款总数为
S20+150= (元)。
(元)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com