7. 已知A={x|x²－3x+2≤0}，B={x|x²－(a+1)x+a≤0}。

1)若AB，求a的取值范围；

2)若BA，求a的取值范围；

3)若A∩B中反含有一个元素，求a的数值。

解：A={x|x²－3x+2≤0}={x|1≤x≤2}

B={x|x²－(a+1)x+a≤0}=　 {x|1≤x≤a}(当a≥1时)

{x|a≤x≤1}(当a＜1时)

1)∵AB

∴易知a≥1

将A与B在同一数轴上表示出来得：

∴易知a＞2。

2)∵BA

∴易知a≥1

将A与B在同一数轴上表示为：

∴易知1≤a＜2。

3)∵1∈A、1∈B，A∩B中反含一个元素

∴A∩B={1}

∴a≤1。

点评：在处理集合之间的关系和集合的运算问题时，能将集合化简的要尽量化简，能用图形直观表示的要尽量采用，这样会使问题难度大大降低。

6. 如果全集I={x|x为小于20的非负偶数}，并且A∩B={4，8，16}， A∩B={10，14，18}，A∩B =Φ，则集合 A∪B =　　　　　　 。

答案：{4，8，10，14，16，18}

评析：将本题所涉及的集合用维恩图表示出来，则其中的关系会直观地显示出来。如图：

Ⅰ表示A∩B，“Ⅰ+Ⅱ”表示B，“Ⅰ+Ⅲ”表示A。

Ⅱ为B∩A　，Ⅲ为A∩B，Ⅳ表示A∩B。

将各数填至相应部分即得答案。

5. 若不等式|x+1|≥kx对x∈R恒成立，则x的取值范围是：　　　　 。

答案：0＜k＜1或k＞－1

点评：将本题转化为函数问题解决，共设y₁=|x+1|，y₂=kx，易知y₁=|x+1|的图象为一条折线，y₂=kx为过原点的一直

4. 已知集合；A∩R⁺=，则实数P的取值范围是　　　　 。

答案：0＜P＜4

点评：“A∩R⁺=”　 “Δ＜0或x₁＜0，x₂＜0”所以本题是求集合，

的并集，其中，={P|x₁+x₂＜0，且x₁x₂＜0}=Φ，所以答案为0＜P＜4

3. 条件甲：P∩Q=P，条件乙：PQ，那么(　　 )

(A)甲是乙的充分而不必要条件

(B)甲是乙的必要而不充分条件

(C)甲是乙的充分且必要条件

(D)甲既不是乙的充分条件，也不是乙的必要条件。

答案：(B)

点评： 由P∩Q=P，则既可能PQ，也可能P=Q，因而得不出甲　　 乙，故甲不是乙的充分条件；但由PQ，必有P∩Q=P，因而乙　 甲，故，甲是乙的必要条件。

2. 在三个关于x的方程x²+ax+4=0，x²+(a－1)x+16=0，x²+2ax+6a+16=0，至少有一个方程有实根，则实数a的取值范围是(　　 )

(A)－4≤a≤4　　　　　　 (B)－2＜a＜4

(C)a≤－2或a≥4　　　　 (D)a＜0

答案：(C)

点评：“三个方程至少有一个方程有实根”等价于“三个判别式至少有一个大于等于0”所以本题是求集合{a|a²－16≥0}；{a|(a－1)²－64≥0；{a|4a²－4(6a+16)≥0}的并集，而不是交集，即不是解不等式组

1. 已知I为全集，集合M，NI，若M∩N=N，则(　　 )。

(A)C_IMC_IN　　　　　 (B)MC_IN

(C)C_IMC_IN　　　　　 (D)MC_IN

答案：(A)

点评：本题涉及M、N、I、C_IM、C_IN五个集合之间的关系，若直接应用逻辑推理较为抽象，我们用维恩图表示出各集合的关系，答案就会一目了然。

2．定义域x∈(-1，+∞)，任取-1＜x₁＜x₂＜+∞，则

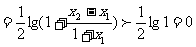，故f(x)单增

4．，(x＞1或x＜-1)；5．x=y=-1．

2．求出函数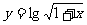的定义域，再证明在定义域内，它是单调增函数．

对数函数答案