
题目列表(包括答案和解析)
10、已知集合M={X|x=12m+8n+4l,m,n,2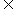 z}与N={X|=209+169+12r,p,q,r
z}与N={X|=209+169+12r,p,q,r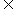 z}求证:M=N
z}求证:M=N
解:(1)证M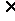 N
N
对任意的x0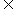 M,则必存在m0,n0,l0
M,则必存在m0,n0,l0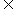 z, 有x0=12 m0+8no+4L0
z, 有x0=12 m0+8no+4L0
=20n0+16l0+12(m0-n0-L0)
∵n0, L0,m0-n0-L0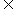 z
z
∴x0℃N
∴M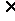 N
N
(2)证N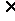 M
M
对任意的X N,则必存在P0,q0,XZ有x0=20P0+16q0+12r0=12r0+(2q0+4(5q0)
N,则必存在P0,q0,XZ有x0=20P0+16q0+12r0=12r0+(2q0+4(5q0)
综上所得:M=N
点评:将系数为12,8,4的代数式与系数为20,16,12的代数式互相转化是解题的难点也是关键点;为解决这个难点可采用待定系数法,如设12mo+8no+4l0=20(q1m0+b,no+cl0)+16(q2m0+b2n0+c2l0)+12(a3mo+b3mo+c3lo)所以得到
12=20a1+16a1+12a3
8=20b1+16d2+12b3
4=20q1+16c2+12c3
只要求出每个方程的一组整数解即可!
9、设集合m={1,2,3……1000},对M的任一空子集X,令ax表示出中最大数与最小数之和,那么所有这样的ax的算术平均值是 。
略解:若A={a1a2…an} M
M
则 B={1001-a1,1001-a2….1001-am} M
M
∴aA=a1+am, aB=(1001-a1)+(1001-am)
∴aA+aB=2002
若A=B,则aA=aB=1001
∴所有这样ax的算术平均值为1001。
点评:构造A、B这两种对应集合是解题关键。
8、集合M=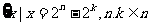 且n>k
且n>k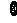 则集合p=
则集合p= ≤x≤2000且x
≤x≤2000且x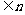
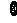 则集合M∩P中所整元素的和为
。
则集合M∩P中所整元素的和为
。
略解: ∵ X≥1901
∴2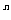 >1901
>1901
∴n≥11
当n=12时,2 -2
-2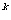 的最小值为2
的最小值为2 -2
-2 =2048>2000
=2048>2000
∴n=11 进一步推理易知 k=7或6,
∴ M∩P={2 -2
-2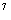 ,2
,2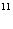 -2
-2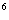 }={1920,1984}
}={1920,1984}

∴M∩P=中各元素的和为 1920,1984=3904
点评:运用不等式控制的方法求出N的值是解题关键。
7、已知I=R,集合A、B都是实数集I的子集。



 A∩B
A∩B {x|x2<4=,A∩B={x1}(x-4)(8-x)≥0
{x|x2<4=,A∩B={x1}(x-4)(8-x)≥0 , A∩B={x|x2-6X-16>0}
, A∩B={x|x2-6X-16>0}
求则A∩B=
 略解: A∩B=
略解: A∩B=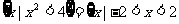
 A∩B=
A∩B= (x-4)(8-x)≥0
(x-4)(8-x)≥0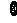 =
=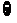 x|4≤x≤8
x|4≤x≤8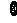


 A∩B=
A∩B= =
=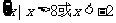
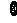




 由维思图易知 A∩B=(A∩B) ∪(A∩B) ∪(A∩B)
由维思图易知 A∩B=(A∩B) ∪(A∩B) ∪(A∩B)






 将A∩B,A∩B,A∩B 分别画在同一条轴上,易知:(A∩B)∪(A∩B)∪(A∩B)
将A∩B,A∩B,A∩B 分别画在同一条轴上,易知:(A∩B)∪(A∩B)∪(A∩B)
=≥ ≥4或x≤2
≥4或x≤2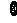 ∴A∩B=
∴A∩B=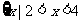
点评:本题涉及的各集合的关系较多,采用维思图和数轴表会使基间的各种关系较为直观。




 其中A∩B= A∩B)∪(A∩B)∪(A∩B这一关系式可由集合的基本运算推出。
其中A∩B= A∩B)∪(A∩B)∪(A∩B这一关系式可由集合的基本运算推出。
6.在坐标平面内,纵横坐标都是整数的点,叫做整点,我们用I表示所有直线的集合,M表示恰好通过一个整点的直线的集合,N表示不通过任何整点的直线的集合,p表示通过无穷整点的直线的集合,那么表达式正确的有几个( )
(1) M∪N∪P=I
(2)
N≠

(3)
M≠
(4)
P≠
(A) 1 (B) 2 (C) 3 (D)4
答案:(D)
点评:本题易构造出y= x,y=
x,y= ,
,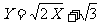 ,Y=X来说明(2)、(3)、(4)均是正确的,所以本题的难点在于证明过两个整点的直线一定过无数个整点:设直线ax+by=G过整点(Xo,yo),(xo,yo)易证直线必过整点((n+1)xo-xo,(n+1yo-yo)所以直线ay+by=必过无数个整点。
,Y=X来说明(2)、(3)、(4)均是正确的,所以本题的难点在于证明过两个整点的直线一定过无数个整点:设直线ax+by=G过整点(Xo,yo),(xo,yo)易证直线必过整点((n+1)xo-xo,(n+1yo-yo)所以直线ay+by=必过无数个整点。
5. 关于X的二次方程 +(a
+(a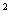 -1)x+a-2=0的一个根比1大,另一个根比1小的充要条件是( )
-1)x+a-2=0的一个根比1大,另一个根比1小的充要条件是( )
(A) -1<a<1 (b) a<-1或a>1
(C) -2<a<1 (d) a<-2或a>1
略解(一)设函数y=f(x)=  +( a
+( a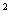 -1)x+(a-2)
-1)x+(a-2)
由函数图象易知:方程 +( a
+( a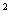 -1)x+a-2=0的一个根比1大,
-1)x+a-2=0的一个根比1大,
一个根比1小 óf(1)<0 ó 1+( a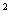 -1)+a-2<0
-1)+a-2<0
ó-2<a<1 故选(C)
略解(二)设方程式的两个根为X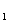 ,X
,X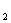 X
X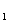 >1> X
>1> X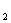
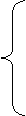
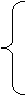
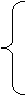 则
则  △>0
△>0
 △>0
△>0
△>0
△>0
X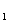 >1 ó (X
>1 ó (X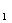 -1)>0 ó ó-2<a<1
-1)>0 ó ó-2<a<1
X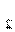 <1
(x
<1
(x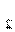 -1)<0
(x
-1)<0
(x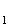 -1)( x2 –1)<0
-1)( x2 –1)<0
2、存在一个元素a,a∈m, a N.
N.
4. M=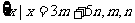 ∈z
∈z .N=
.N= ∈z
∈z

那末M与N的关系是( )
(A) M=N (B) M N (C) M
N (C) M (D)M∩N=
(D)M∩N=
略解1:集合M中同时含有奇数、偶数;集合N中仅含偶数,
所以 (A)(B) 一定是错误的,又因8∈M,8∈N
 ∵M∩N=
∵M∩N= ∴(D) 错误 由排除法得答案为 C
∴(D) 错误 由排除法得答案为 C
略解2 对任意的X0∈N,则必存在着m0 n0∈z
若 X0=2 m0+4n0 =3(-m0 -2 n0)+5( m0+2n0)
∵-m0 -2 n0∈z, m0+2n0∈z
∴X0∈M
∴N M
M
又∵ 3∈M,3 N
N
∴N 故选C
故选C
点评:解法I比较了集合M,N中等部分元素运用排除法得到了答案;解法2从一般性出发对M 进了行论证。 注证 M
进了行论证。 注证 M 需证:1、 M
需证:1、 M
3. I为全集,集合A,B 满足A∪B=I,那么





 (1)A∩B=
(1)A∩B= , (2) A∩B=B (3)A∪B=A (4)B> A
, (2) A∩B=B (3)A∪B=A (4)B> A
四个关系中正确的个数是
(A) 1 (B)2 (C) 3 (D)4
略解:

 1)
1)
 ∩
∩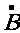 =A ∩B = I=
=A ∩B = I= 


 (2) A∪B=I=>A=B=>A∩B= B
(2) A∪B=I=>A=B=>A∩B= B

 (3) A∪B=I=>B=A=>
A∪B=A
(3) A∪B=I=>B=A=>
A∪B=A

 (4) A∪B=I=>B=A=> B> A
(4) A∪B=I=>B=A=> B> A
所以 (1),(2),(3),(4) 都正确 顾选 D
点评:本题主要考察集合间的 交 并 补运算,本题若从维恩图入手更为简捷.
2.已知X∈R,Y∈R 集合A=
集合A=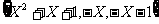 ,
,
集合 B=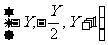 ,若A=B,则
,若A=B,则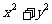 的值是( )
的值是( )
(A) 5 (B) 4 (C)25 (D)10
略解:易知-x-1<-x≤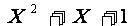
∵Y∈R ,∴-y<
,∴-y<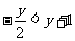
∵A=B
∴



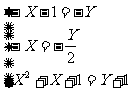 =>
=>


经检验 x=1,y=2 满足集合元素的互异性,所以x2+y2=5
点评:将两个集合中的元素分别按大小关系排序后寻找对应关系是解本题的关键.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com