
题目列表(包括答案和解析)
3.若p:x>1 q:x2>1,则p 是q 的什么条件( ).
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)非充分也非必要条件
 [提示]p
[提示]p  q 但q q.
q 但q q.
[答案](A).
2.设A= x|x<2
x|x<2 ,B=
,B= x|x2<4
x|x2<4 ,则下列各式正确的是( ).
,则下列各式正确的是( ).
(A)A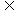 B (B)A
B (B)A B (C)A=B (C)B
B (C)A=B (C)B A
A
[提示]B= x|-2<x<2
x|-2<x<2 .
.
[答案](B).
1.下列各命题,正确的为( ).
(A)0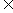
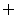 (B)
(B)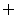
 {0} (C)
{0} (C)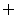 ={0} (D)
={0} (D)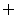
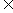 {0}
{0}
[提示]注意空集为任何非空集合的真子集.
[答案](B).
1 下列各集合中,与集合{x|x2=1,x∈R}不相等的集合为( )。
 (A){1,-1}
(B){x| |x|=1,x∈R}
(A){1,-1}
(B){x| |x|=1,x∈R}
 (C){x| x=
(C){x| x=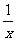 ,x∈R} (D){x| x3=x,x∈R}
,x∈R} (D){x| x3=x,x∈R}
答案:(D)
点评:判断两个集合是否相等,关键是看它们所含的元素是否完全相同。(注:两个相等的集合可以有不同的特征性质,但这不同的性质所决定的元素必须是完全相同的)由于(D)集合含元素比其它四集合的元素多了一个0,所以选(D)。
2 满足{a,b∈M {a、b、c、d、e}的集合M的个数是( )。
{a、b、c、d、e}的集合M的个数是( )。
(A)2个 (B)4个 (C)7个 (D)8个
答案:(C)
点评:本题主要考查子集与真子集的概念,由题意易知集合M至少由{a、b、c、d、e}中的二个元素a、b组成,但又不能同时有这5个元素,所以M共有如下七种情况{a、b};
{a、b、c};{a、b、d};{a、b、e};{a、b、c、d};{a、b、c、e};{a、b、d、e}。
3 若关于x的一元二次不等式ax2+bx+c<0的解集为实数集R,则a、b、c应满足的条件为( )。
(A)a>0,b2―4ac>0 (B) a>0,b2―4ac<0
(C) a<0,b2―4ac>0 (D) a<0,b2―4ac<0
答案:(D)
点评:本题主要考查一元二次不等式与一元二次函数间的内在联系;“求不等式ax2+bx+c<0的解集”等价于“问,当x为何值时,函数y=ax2+bx+c值小于0”所以由题意知:y=ax2+bx+c(a≠0)的图象开口向下,且与x轴无交点,故选(D)。
4 若集合A={a、b、c}则集合A的子集共有 个。
答案: 8 。
点评:注意不要漏掉φ与A 。
5 已知集合A有10个元素,集合B有8个元素,集合有4个元素,则集合A B有
个元素。
B有
个元素。
答案: 14 。
点评:由维恩图易知n(A B)=n(A)+n(B)―n(A
B)=n(A)+n(B)―n(A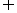 B)所以 n(A
B)所以 n(A B)=10+8-4=14 (注:n(A)表示集合A 中元素的个数)。
B)=10+8-4=14 (注:n(A)表示集合A 中元素的个数)。
6 已知A x| 0<x<3
x| 0<x<3 ,B=
,B= x|x≥a
x|x≥a 若A
若A B,则a的取值范围是: 。
B,则a的取值范围是: 。
答案:a≥3
点评:将集合A、B分别在同一数轴表示出来为:
因为A B,所以a的最小值为3。
B,所以a的最小值为3。
7 解不等式6x2<x+2
解:将不等式转化为6x2+ x+2>0
∵方程6x2+ x+2=0的两根为x1=- ,x2=
,x2=
∴不等式6x2+ x+2>0的解集为 x| x<-
x| x<- 或x>
或x>

∴原不等式的解集为 x| x<-或x>
x| x<-或x>

点评:对于一元二次不等式6x2+ x+2>0(<0)的解法,我们通常是将其先转化为a>
0的情况来处理。
8 已知m<0,求|mx|-2<0的解集。
解:|mx|-2<0  m<0
m<0
 |mx|<2
|mx|<2  m<0
m<0


 m<0
m<0


∴不等式|mx|-2<0的解集为 x|
x| <x<
<x<

点评:在解不等式时要注意每一步都必须是等价转化。
9 已知集合A={a2,a+1,-3},B={a-3,2a-1,a2+1}且A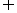 B={-3},求实数a的值。
B={-3},求实数a的值。
解:∵A∩B={-3}
∴-3 B
B
1)若a-3=3,则a=0,则A={0,1,-3},B={-3,-1,1}
∴A∩B={-3,1}与A∩B={-3}矛盾,所以a-3≠-3。
2)若2a-1=-3,则a=-1,则A={1,0,-3},B={-4,-3,2}
此时A∩B={-3}符合题意,所以a=-1。
点评:本题在解题过程中采用的是指出关系,所以最后应检验所求出的a值是否符合题意。
10. 用反证法证明:若a>b>0,则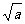 >
>
证明:假设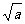 <
<
∴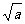 -
- <0
<0
∴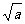 +
+ >0
>0
∴(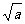 -
- )(
)(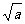 +
+ )<0
)<0
∴a-b<0
∴a<b 这与a>b矛盾,所以假设不成立,即原命题为真。
点评:用反证法证明一般分三步:①假设原命题的后命题为真;②在①的基础上进行推理,直至推出与已知条件或原已有的公理、定理矛盾为止;③根据反证法原理得原命题为真。
3.设A={xy| ≤1},Bm={x,y|y=-(x-m)2+2 m},B=
≤1},Bm={x,y|y=-(x-m)2+2 m},B=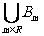 ,求A
,求A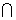 B的面积.
B的面积.
[解]集合A可以看作是以(0,1)为圆心,以1为半径的圆及圆内所有点的集合;
Bm表示以(m,2m)为顶点,形状与 相同的抛物线;
相同的抛物线;
B表示当m运动变化时,得到的所有Bm的并集,如图。
 当 变化时,Bm的顶点的轨迹为一条直线
当 变化时,Bm的顶点的轨迹为一条直线 。
。
设直线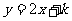 与抛物线y=-(x-m)2+2 m相切
与抛物线y=-(x-m)2+2 m相切
∴ 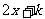 =-(x-m)2+2 m
=-(x-m)2+2 m

∴ Δ=
即 
k=1
∴ B表示直线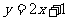 以下的部分(含
以下的部分(含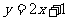 上的点)
上的点)
∵ 点(0,1)在直线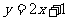 上
上
∴ A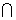 B即为半圆.
B即为半圆.
∴ A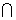 B的面积为
B的面积为 .
.
2.设M={1,2,3,…,1995},A是M的子集,且满足条件:若k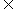 A时,则15k不属于A,求A中最多能有多少个元素?
A时,则15k不属于A,求A中最多能有多少个元素?
[解](1)构造125个数组:(9,9×15);(10,10×15),…,(133,19×15)
由条件知A中不能同时包含任一数组中的两个数,所以A中元素的个数不会超过1995-125=1870个
(2)当A={1,2,…,8,134,135,…1995}时满足条件,所以A中元素可达1870个
综合(1)(2)知,A中最多有1870个元素。
1.已知集合M={x|x=12 m+8 n+4 k,m、n、k 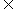 Z}与N={x|20 p+16 q+12 r,p、q、r
Z}与N={x|20 p+16 q+12 r,p、q、r 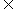 Z},求证:M=N.
Z},求证:M=N.
[证明]
(1)证M N
N
对任意的x0 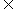 M, 则必存在m0、n0、k0
M, 则必存在m0、n0、k0 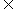 Z,使x0=12 m0+8 n0+4 k0
Z,使x0=12 m0+8 n0+4 k0
=20 n0+16 l0+12(m0-n0-k0)
∵ n0,k0,m0-n0-k0 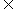 Z
Z
∴ x0 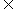 N.
N.
∴ M N.
N.
(2)证N M
M
对任意的x0  N,则必存在p0、q0、r0,使x0=20 p0+16 q0+12 r0=12(r0+p0+q0)+8 p0+4 q0.
N,则必存在p0、q0、r0,使x0=20 p0+16 q0+12 r0=12(r0+p0+q0)+8 p0+4 q0.
∴ x0  M.
M.
∴ N M.
M.
综上知,M=N.
[点评]将系数为12,8,4的代数式与系数为20,16,12的代数式互相转化是解题的难点也是关键,为解决这个难点可采用待定系数法.
5.已知I={(x,y)|x,y  R},A={(x,y)|y=3 x-2},B={(x,y)|
R},A={(x,y)|y=3 x-2},B={(x,y)|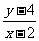 =3},则
=3},则 IA
IA B=____________.
B=____________.
[提示]B={(x,y)|y=3 x-2,x≠2}.
[答案]{(x,y)|x,y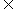 R且(x,y)≠(2,4)}.
R且(x,y)≠(2,4)}.
4.已知集合A={x|x=a2+1,a 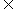 N+},B={y|y=b2-6 b+10,b
N+},B={y|y=b2-6 b+10,b 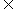 N+},则A与B的关系为________________.
N+},则A与B的关系为________________.
[提示]B={y|y=(b-3)2+1,b 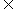 N+},当b=4,5,6,…时,y 的值与集合A中a=1,2,…时,x的值相同,而b=3时,y=1
N+},当b=4,5,6,…时,y 的值与集合A中a=1,2,…时,x的值相同,而b=3时,y=1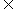 B,但1
B,但1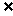 A.
A.
[答案]A B.
B.
3.已知集合A={(x,y)|y=ax+2},B={(x,y)|y=|x+1|},且A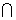 B是一个单元集,则实数a 的取值范围为________________.
B是一个单元集,则实数a 的取值范围为________________.
[提示]运用函数图象.
[答案] -∞,-1
-∞,-1

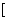 1,+∞
1,+∞ .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com