
题目列表(包括答案和解析)
4.已知向量 与
与 不共线,
不共线,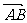 =
= +k
+k ,
, =l
=l +
+ (k,l∈R),则
(k,l∈R),则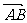 与
与 共线的条件是( ).
共线的条件是( ).
(A)k +l =0 (B)k -l =0
(C)kl+1=0 (D)kl-1=0
[提示]
∵ 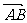 ∥
∥ ,
,
∴  +k
+k =l(l
=l(l +
+ ) (l∈R)
) (l∈R)
即 (1-ll) +(k -l)
+(k -l) =
=
∵  、
、 不共线,则
不共线,则
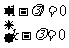 ,消去l,
,消去l,
∴ kl-1=0.
[答案](D).
[点评]
本题考查向量共线的充要条件、向量相等的充要条件及逻辑推理能力.即引入l后,再设法消去l,寻求k与l的关系式.
3.已知 =(-2,3),
=(-2,3), =(3,2),若m1=
=(3,2),若m1= ·
· ,m2=
,m2= ·(
·( +
+ ),m3=
),m3= (
( +
+ ),m4=(
),m4=( +
+ )(
)( -
- ),m5=(
),m5=( +
+ )2,则m1,m2,m3,m4,m5的大小顺序是( ).
)2,则m1,m2,m3,m4,m5的大小顺序是( ).
(A)m1<m2=m3<m4<m5
(B)m1<m3=m4<m2<m5
(C)m1=m4<m2=m3<m5
(D)m1=m5<m4=m2<m3
[提示]
利用向量的坐标运算,分别计算出m1=(-2)×3+3×2=0,m2=(-2)×1+3×5=13,m3=3×1+2×5=13,m4=1×(-5)+5×1=0,m5=26,于是m1=m4<m2=m3<m5.
[答案](C).
[点评]本题主要考查向量的坐标运算及计算能力.
2.已知向量 =
= 1,0),
1,0), =(0,1),则与2
=(0,1),则与2 +
+ 垂直的向量是( ).
垂直的向量是( ).
(A)2 -
- (B)
(B) -2
-2
(C)2 +
+ (D)
(D) +2
+2
[提示一]
利用向量的坐标计算
∵  =(1,0),
=(1,0), =(0,1),
=(0,1),
∴ 2 +
+ =(2,1)
=(2,1)
而 -2
-2 =(1,-2)
=(1,-2)
有(2 +
+ )(
)( -2
-2 )=2×1+(-2)×1=0,
)=2×1+(-2)×1=0,
∴ (2 +
+ )⊥(
)⊥( -2
-2 ).
).
[提示二]
利用向量的运算
由已知,得| |=1,|
|=1,| |=1,
|=1, ·
· =0,
=0,
∴ (2 +
+ )(
)( -2
-2 )=2
)=2 -3
-3 ·
· -2
-2 =0,
=0,
∴ (2 +
+ )⊥(
)⊥( -2
-2 ).
).

[提示三]
利用向量的几何意义.由已知,可得 与
与 是互相垂直的单位向量.
是互相垂直的单位向量.
如图,在直角坐标系中,2 +
+ =
=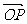 .
.

显然 2 -
- 表示的向量
表示的向量 不与
不与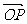 垂直,2
垂直,2 +
+ 表示的向量
表示的向量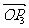 与
与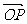 重合;
重合; +2
+2 表示的向量
表示的向量 也不与
也不与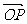 垂直.
垂直.
[答案](B).
[点评]
本题主要考查向量垂直的充要条件.通常有三种方法,一是利用向量的坐标运算;二是利用向量的运算,三是利用向量的几何意义.
1.设 、
、 、
、 是任意的非零平面向量,且相互不共线,则
是任意的非零平面向量,且相互不共线,则
①( ·
· )
) -(
-( ·
· )
) =
= ;
;
② | |-|
|-| |<|
|<| -
- |;
|;
③( ·
· )
) -(
-( ·
· )
) 不与
不与 垂直;
垂直;
④(3 +2
+2 )·(3
)·(3 -2
-2 )=9|
)=9| |2-4|
|2-4| |2
|2
中,是真命题的有
(A)①② (B)②③ (C)③④ (D)②④
[提示]
对于②,| |、|
|、| |,|
|,| -
- |表示三角形的三条边长,可得|
|表示三角形的三条边长,可得| |-|
|-| |<|
|<| -
- |,故②是正确的,排除(C);对于④,利用向量的运算,可得④正确的.
|,故②是正确的,排除(C);对于④,利用向量的运算,可得④正确的.
[答案](D).
[点评]
本题考查平面向量中零向量、共线向量、向量的垂直、向量的横等有关概念和向量的加、减、与实数的积,数量积这些基本的运算及其运算性质.因为向量的数量积不满足结合律,即( ·
· )·
)· ≠
≠ ·(
·( ·
· ),故命题①是错误的;而对于[(
),故命题①是错误的;而对于[( ·
· )
) -(
-( ·
· )
) ]·
]· =(
=( ·
· )
) ·
· -(
-( ·
· )
) ·
· =0,有(
=0,有( ·
· )
) -(
-( ·
· )
) 与
与 是垂直的,故命题③是错误的.
是垂直的,故命题③是错误的.
2.在△ABC中,a +b =10,而cos C是方程2 x2-3 x -2=0的一个根,求△ABC周长的最小值.
[提示]
三角形周长为a +b +c,而a +b =10已知,故求△ABC周长的最小值.就是求C的最小值,由方程的根可解得cos C的值,借助余弦定理得c与a(或b)的关系,再确定C的最小值.
[答案]
解方程2 x2-3 x -2=0,得
x =2或x =- .
.
∵ |cos C|≤1,
∴ cos C
=- .
.
由余弦定理,得
c2=a2+b2-2 ab cos C
=a2-b2+ab
=(a +b) 2-ab,
而 a +b =10,
∴ c2=100-a(10-a)
=a2-10 a +100
=(a -5)2+75.
∴ 当a =5时,c有最小值 =5
=5 .
.
∴ △ABC的周长为 10+5 .
.
[点评]
本题综合考查余弦定理,二次函数的极值等内容.通过分析题目已知条件,将求三角形周长最小值问题转化为求c边的最小值问题.借助已知条件和余弦定理,建立了关于a的二次函数关系,利用二次函数最值的结论确定出c的最小值,使向量得解.在解决问题的过程也考查分析问题.解决问题的能力.
1.已知P为△ABC内一点,且3 +4
+4 +5
+5 =
= .延长AP交BC于点D,若
.延长AP交BC于点D,若 =
= ,
, =
= ,用
,用 、
、 表示向量
表示向量 、
、 .
.
[提示]
注意到 =
= -
- ,
, =
= -
- ,由已知3
,由已知3 +4
+4 +5
+5 =
= ,可以得到
,可以得到 关于
关于 、
、 的表达式,化简即可.对于
的表达式,化简即可.对于 ,可利用
,可利用 与
与 共线予以解决.
共线予以解决.
[答案]
∵  =
= -
- =
= -
- ,
,
 =
= -
- =
= -
- ,
,
又 3 +4
+4 +5
+5 =
= ,
,
∴ 3 +4(
+4( -
- )+5(
)+5( -
- )=
)= ,
,
化简,得 =
=
 +
+
 .
.
设 =t
=t (t∈R),则
(t∈R),则
 =
= t
t  +
+ t
t . ①
. ①
又设  =k
=k (k∈R),
(k∈R),
由  =
= -
- =
= -
- ,得
,得
 =k(
=k( -
- ).
).
而  =
= +
+ =
= +
+ ,
,
∴  =
= +k(
+k( -
- )
)
=(1-k) +k
+k ②
②
由①、②,得
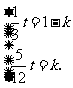 解得 t =
解得 t =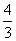 .
.
代入①,有
 =
=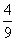
 +
+
 .
.
[点评]
本题是以 、
、 为一组基底,寻求
为一组基底,寻求 、
、 关于
关于 、
、 的线性分解式,主要考查了向量的加法.实数与向量的积及运算律,两个向量共线的充要条件,平面向量基本定理,求
的线性分解式,主要考查了向量的加法.实数与向量的积及运算律,两个向量共线的充要条件,平面向量基本定理,求 时,利用了以
时,利用了以 、
、 为基底的
为基底的 的分解式是唯一确定的,这是求线性分解式常用的方法.
的分解式是唯一确定的,这是求线性分解式常用的方法.
5.在△ABC中,B =30°,AB =2 ,S△ABC=
,S△ABC= ,则AC的长等于_______.
,则AC的长等于_______.
[提示]由已知,S△ABC= AB · BC · sin B =
AB · BC · sin B = ×2
×2 ×BC · sin 30°,得
×BC · sin 30°,得 BC =
BC = ,于是BC =2.
,于是BC =2.
代入余弦定理,得
AC 2=AB2+BC2-2 AB · BC · cos B =4.
∴ AC =2.
[答案]2.
[点评]本题考查余弦定理的应用,在△ABC中,先由面积求出BC,问题转化为已知两边及一夹角.求第三边,应用余弦定理.
4.把函数y =2 x2+x +3的图象C按 =(3,-1)平移到C′,则C′的函数解析式为______.
=(3,-1)平移到C′,则C′的函数解析式为______.
[提示]
利用平移公式,设P(x,y)为函数y =2 x2+x +3图象C上的任一点,经 平移后,对应点P′(x′,y′)在C′上,则
平移后,对应点P′(x′,y′)在C′上,则
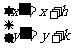 即
即
代入C的方程,得
y′+1=2 (x′-3)2+(x′-3)+3.
即y′=2 x′2-13 x′+17.
[答案]y′=2 x2-13 x +17.
[点评]本题考查平移公式,注意移图是在确定的坐标系xOy内进行的,习惯上将x′,y′仍写成x,y,于是C′的函数解析式为x,y的关系式.
3.在△ABC中,已知B =135°,C =15°,a =5这个三角形的最大边长为______.
[提示]
由已知B =135°为三角形中的最大角,其对边b为所求的最大边.
先由已知的B =135°,C =15°,求得
A =180°-(B +C)=30°.
再由正弦定理,得
b =
=
=5 .
.
∴ △ABC的最大边长为5 .
.
[答案]5 .
.
[点评]本题主要考查应用正弦定理解决三角形的有关问题.
2.已知A(2,3),B(-1,5),且 =
=
 ,
, =-
=-
 ,则CD中点的坐标是________.
,则CD中点的坐标是________.
[提示]
要求CD中点的坐标,必先求得点C、D的坐标.
∵ A(2,3),B(-1,5).
∴  =(-3,2),
=(-3,2),
∴  =
=
 =(-1,
=(-1,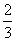 ).
).
则点C的坐标为(1, ).
).
又 =-
=-
 =(
=( ,-
,- )
)
由点D的坐标为( ,
, )
)
代入中点坐标公式,得
(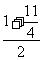 ,
,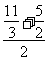 ),即(
),即(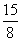 ,
, ).
).
[答案](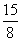 ,
, ).
).
[点评]本题考查共线向量,向量的坐标运算及线段的定比分点的坐标公式.本题也可代入线段的定比分点的坐标公式.由 =
=
 ,得
,得 =
=
 ,即点C分
,即点C分 所成的比为
所成的比为 ,可得点C的坐标;由
,可得点C的坐标;由 =-
=-
 ,得
,得 =-
=-
 ,即点D分
,即点D分 所成的比为-
所成的比为- ,可得点D的坐标.
,可得点D的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com