
题目列表(包括答案和解析)
3.设锐角△ABC的外接圆圆心为O,边BC的中点为M,自顶点向BC引垂线,垂足为D,并在垂线上取一点H,与M在AO的同一侧,使得AH =2 OM,若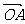 =
= ,
, =
= ,
,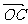 =
= .
.
(1)试用 、
、 、
、 表示
表示 、
、 ;
;
(2)据(1)的结论,证明BH ⊥AC,CH ⊥AB.

[提示]
(1)用 、
、 、
、 表示
表示 、
、 ,即寻求
,即寻求 ,
, 关于
关于 、
、 、
、 的线性分解式,在△BOC中,可得
的线性分解式,在△BOC中,可得 ,再利用
,再利用 =2
=2 ,而
,而 =
= +
+ ,得
,得 ;(2)要证BH ⊥AC,只需证明
;(2)要证BH ⊥AC,只需证明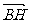 ·
·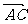 =0,用
=0,用 、
、 、
、 表示
表示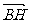 ,
,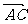 ,化简即可,同理可证CH ⊥AB.
,化简即可,同理可证CH ⊥AB.
[答案]
(1)在△BOC中,M为BC的中点,
∴  =
= (
( +
+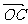 )=
)= (
( +
+ ).
).
∵  =2
=2 ,
,
∴  =
= +
+ ,
,
∴  =
= -
- =
= +
+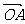 =
= +
+ +
+ ,
,
(2)∵ 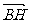 =
= +
+ =-
=- +(
+( +
+ +
+ )=
)= +
+ ,
,
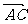 =
= +
+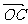 =-
=- +
+ ,
,
∴ 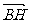 ·
·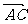 =(
=( +
+ )(-
)(- +
+ )=|
)=| |2-|
|2-| |2
|2
又 O为△ABC外接圆的圆心,有
| |=|
|=| |=|
|=| |.
|.
∴ 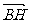 ·
·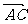 =0,即 BH
⊥AC.
=0,即 BH
⊥AC.
同理,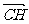 =
= +
+ ,
, =
= -
- ,
,
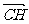 ·
· =(
=( +
+ )(
)( -
- )=|
)=| |2-|
|2-| |2=0,
|2=0,
∴ CH ⊥AB.
[点评]本题考查向量的加减法及运算律,向量的基本定理及向量垂直的充要条件,考查逻辑推理能力.
2.如图,在四边ABCD中,BC =a,DC =2 a,四个内角A、B、C、D的度数的比为
3︰7︰4︰10,求AB的长.

[提示]
由于AB在△ABD中,寻求使△ABD有解的条件是关键,据四边形内角和为360°及四个内角之比,可求得四个内角.此时△BDC便是已知两边BC、DC及夹角C.于是这个三角形可解.借助△BDC可以求的BD,∠ACB用正弦定理可得AB.
[解]连BD,设四个角A、B、C、D的度数分别为3 x,7 x,4 x,10 x.则由四边形内角和,有3 x +7 x +4 x +10 x =360°
∴ x =15°.
∴ A =45°,B =105°,C =60°,D =150°.
在△BCD中,由余弦定理,得
BD2=BC2+CD2-2 BC · CD cos C
=a 2+4 a 2-2 a · 2 a ·
=3 a2.
∴ BD
= a.
a.
这时有,BD2+BC2=DC2,则△BDC为直角三角形,∠DBC =90°.
∴ ∠CDB =30°.
于是 ∠ADB =120°.
在△ADB中,由正弦定理,得
AB =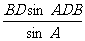
=
=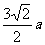 .
.
[点评]
本题重点考查正弦定理,余弦定理及解斜三角形的基本方法、题目的已知条件以四边形为背景给出.实际四个内角和两条边已知,去求另外一边AB.一般的思路将所求的边AB放在三角形内,求解这个三角形是问题解决的核心,这就需要根据已知条件寻求解决AB所在三角形的充分条件.该找边的找边、该求角的求角.解决问题过程中,还需注意设计好演算程序,先求谁,后求谁,再求谁.显得思路清晰、演算合理.
1.在△ABC中,A =120°,sin B ∶ sin
C =3︰2,S△ABC=6 ,求a.
,求a.
[提示]
在△ABC中,要求a的值,已知A,应用余弦定理,只需求得b,c的长.由sin B∶sin C =3∶2,应用正弦定理,可将角的关系转化为b、c边的关系,再利用面积公式,得b、c的另一个关系式,解关于b、c的二元方程组,即可.
[答案]
在△ABC中,由正弦定理,得
 =
=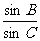 =
=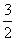 . ①
. ①
又S△ABC= bc sin A =
bc sin A = bc sin 120°=6
bc sin 120°=6 ,
,
于是,bc =24. ②
由①、②,可得b =6,c =4.(负值舍去)
据余弦定理,得
a2=b2+c2-2 bc cos A
=36+16-2×6×4×cos 120°
=76,
∴ a
=2 .
.
[点评]
本题考查应用正弦定理、余弦定理解斜三角形的有关知识.在解三角形时,常常要将正弦定理,余弦定理交替使用,尽管有时不是直接求出结果,但为了过渡,也是很有必要的.
5.求值:sin 2 20°+cos 2 80°+ sin 20°cos 80°=_________.
sin 20°cos 80°=_________.
[提示]
分析原式的结构特点,联想到余弦定理.将其转化为边长的形式,构造三角形可求得原式的值.
[解]由于 cos 80°=sin 10°,则
sin220+cos280°+ sin 20°cos 80°
sin 20°cos 80°
=sin 220°+sin210°+ sin 20°sin 10°.
sin 20°sin 10°.
构造△ABC,使A =20°,B =10°,C =150°,三角形的外接圆半径为R.
则由正弦定理,得a =2 R sin A,b =2 R sin B,c =2 R sin C.
再据余弦定理,有c2=a2+b2-2 ab cos C,
(2 R sin C)2=(2 R sin A)2+(2 R sin B)2-2 (2 R sin A) (2 R sin B) cos C.
即 sin2 C =sin2 A +sin2 B -2 sin A sin B cos C.
sin 2 150°=sin220°+sin210°-2 sin 20°sin 10°cos 150°.
∴ sin2 20°+cos2 80°+ sin 20°cos 80°=
sin 20°cos 80°= .
.
[点评]
本题的解法很多,常用的方法是逆用倍角公式,由 sin220°=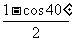 ,cos280°=
,cos280°= ,然后再利用和差化积,积化和差公式,两角和差的三角函数式来化简,一般解题过程较长.前面提供的解法可以说另辟蹊径,据已知三角形函数式结特点,构造三角形,借用余弦定理求解思路新奇,简捷明快.
,然后再利用和差化积,积化和差公式,两角和差的三角函数式来化简,一般解题过程较长.前面提供的解法可以说另辟蹊径,据已知三角形函数式结特点,构造三角形,借用余弦定理求解思路新奇,简捷明快.
4.若向量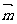 =(
=( ,-1),
,-1),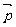 =(
=( ,
,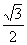 ),
),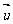 =
=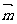 +(x2-3)
+(x2-3)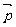 ,
, =-y
=-y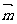 +x
+x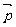 ,且x3-3 x -4 y =0,则
,且x3-3 x -4 y =0,则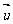 与
与 的夹角等于________.
的夹角等于________.
[提示]要求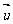 与
与 的夹角,可通过
的夹角,可通过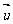 ·
· 来解.据已知,
来解.据已知,
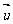 ·
· =-y|
=-y|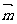 |2+x(x2-3)|
|2+x(x2-3)|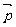 |2+[x -y(x2-3)]
|2+[x -y(x2-3)] 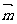 ·
·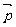 .
.
又 |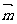 |2=4,|
|2=4,|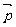 |2=1,
|2=1,
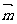 ·
·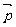 =
= ×
× +(-1)×
+(-1)×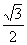 =0.
=0.
∴ 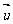 ·
· =-4 y +x3-3 x
=-4 y +x3-3 x
=(x3-3 x)+x3-3 x
=0.
∴ 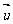 ⊥
⊥ ,即
,即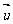 与
与 的夹角为90°.
的夹角为90°.
[答案]90°.
[点评]本题主要考查向量的数量积及运算律.考查计算及逻辑推理能力.
3.将函数y =log3(2 x +1)-4的图象按向量 平移后得到的是函数y =log32x的图象,则
平移后得到的是函数y =log32x的图象,则 的坐标是___________.
的坐标是___________.
[提示]设平移向量 =(h,k).
=(h,k).
由平移公式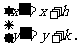 即
即 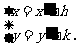
把(x,y)代入y =log3(2 x +1)-4中,得
y′-k =log3[2(x′-h)+1]-4,
即 y′=log3[2 x′+(1-2 h)]+(k -4).
∵ 平移后得到的是函数 y =log32x的图象,
∴  即
即
∴  =(
=( ,4).
,4).
[点评]利用平移可以将复杂函数式转化为简单函数式,这是研究函数的一种重要方法.
2.已知 =(m +1,-3),
=(m +1,-3), =(1,m -1),且(
=(1,m -1),且( +
+ )⊥(
)⊥( -
- ),则m的值是__________.
),则m的值是__________.
[提示]先由向量 、
、 的坐标,求得
的坐标,求得 +
+ =(m +2,m -4),
=(m +2,m -4), -
- =(m,-2-m),再利用向量垂直的充要条件,得(
=(m,-2-m),再利用向量垂直的充要条件,得( +
+ )·(
)·( -
- )=0,即
)=0,即
(m +2)×m+(m -4)×(-2-m)=0,
解出 m =-2.
[答案]-2.
[点评]本题考查向量的坐标运算,向量垂直的充要条件及计算能力.
1.已知平行四边形ABCD的三个顶点A(0,0),B(3,1),C(4,1),则D点的坐标为__________.
[提示]设D(x,y),在□ABCD中,由 =
= ,得
,得
(4-x,3-y)=(3,1)
∴  即
即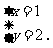
[提示二]
设点O为□ABCD中两条对角线AC、BD的交点.
∵ A(O,O),C(4,3),且O为AC的中点,
∴ O(2,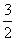 ).
).
又 O为BD的中点,B(3,1),
∴ D(1,2).
[答案](1,2).
[点评]本题考查向量的基础知识及其运算.
求点的坐标的基本方法有两种,一是利用向量的坐标运算,本题提示一利用了相等向量的定义,也可由 =
=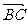 ,求得点D的坐标;二是利用线段的定比分点的坐标公式,提示二的解法利用了中点坐标公式.
,求得点D的坐标;二是利用线段的定比分点的坐标公式,提示二的解法利用了中点坐标公式.
6.在四边形ABCD中,E是AB的中点,K是CD的中点,则以线段AK,CE,BK,DE的中点为顶点的四边形是( ).
(A)任意四边形 (B)平行四边形
(C)矩形 (D)菱形
[提示一]利用坐标法.
设A(a1,a2),B(b1,b2),C(c1,c2),D(d1,d2),则K(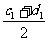 ,
, ),
),
E(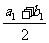 ,
, ),
),
若AK,BK,CE,DE的中点分别为O1,O2,O3,O4,则
O1,O2,O3,O4,则
O1( ,
, ),O2(
),O2( ,
,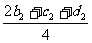 ),
),
O3(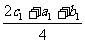 ,
, ),O4(
),O4( ,
, ).
).
于是,
O1O2的中点坐标为( ,
, ),
),
O3O4的中点坐标为( ,
, ).
).
∴ 四边形O1O4O2O3为平行四边形.
利用向量的坐标运算,可进一步验证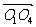 ·
· ≠0,排除(C);
≠0,排除(C); ·
· ≠0,排除(D).
≠0,排除(D).
[提示二]利用向量式
若AK,BK,CE,DE的中点分别为O1,O2,O3,O4,则
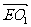 =
= (
( +
+ ),
), =
= (
( +
+ ),
),
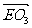 =
=
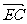 =
= (
( +
+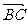 ),
),
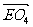 =
=
 =
= (
( +
+ ).
).
∴  =
=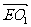 -
-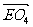
= [(
[( +
+ )-(
)-( +
+ )]
)]
= (
( -
- )
)
= [(
[( +
+ +
+ )-
)- ]
]
= (
( +
+ )
)
= [(
[(
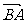 )+(
)+(
 )]
)]
= (
(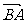 +
+ ).
).
又 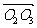 =
=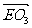 -
-
= [(
[( +
+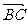 )-(
)-( +
+ )]
)]
= (
(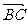 -
- )
)
= [
[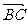 -(
-( +
+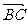 +
+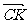 )]
)]
= (-
(- -
-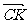 )
)
= [(
[(
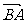 )+(
)+(
 )]
)]
= (
(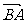 +
+ ).
).
∴  =
=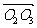 ,即四边形O1O4O2O3是平行四边形.
,即四边形O1O4O2O3是平行四边形.
[答案](B).
[点评]本题主要考查了向量的运算,提示一利用向量的坐标表示及线段的中点坐标公式.将平面几何图形的位置关系转化为坐标的计算问题;提示二利用向量的加、减法运算律,线段中点的向量形式,将问题转化为向量的线性运算,这正体现了向量工具的重要作用之一.
5.设 ,
, ,
, 为平面上的三个向量,且满足
为平面上的三个向量,且满足
 =
= ,
,
 =
=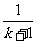 ,
, ·
· =
= (k =1,2),则能使a
(k =1,2),则能使a +b
+b =
= 成立的常数a、b的值是( ).
成立的常数a、b的值是( ).
(A)a =6,b =6 (B)a =-6,b =6
(C)a =6,b =-6 (D)a =-6,b =-6
[提示]要求a、b的值,必需寻求含有a、b的两个关系式.
由已知,得
 ·
· =1,
=1, ·
· =
= ,
, ·
· =
= ,
,
 2=
2= ,
, 2=
2= .
.
对于a +b
+b =
= ,
,
等式两边同乘以 ,得
,得
a 2+b
2+b ·
· =
= ·
· ,
,
即  a +
a + b =1. ①
b =1. ①
等式两边同乘以 ,得
,得
a ·
· +b
+b 2=
2= ·
· ,
,
即  a +
a + b =
b = . ②
. ②
由①、②,可得
a =6,b =-6.
[答案](C).
[点评]本题考查平面向量的数量积及运算律,考查方程的思想方法及逻辑推理能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com