
题目列表(包括答案和解析)
3.已知点P1(1,2),P2(-2,1),直线P1P2与x轴相交于点P,则点P分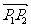 所成的比l 的值为_____.
所成的比l 的值为_____.
[提示]
由直线P1P2与x轴相交于点P,得点P的纵坐标为0,于是0= ,即l =-2.
,即l =-2.
[答案]-2.
[点评]本题考查线段的定比分点的坐标公式.
2.已知A(-1,2),B(2,4),C(4,-3),D(x ,1),若 与
与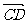 共线,则|
共线,则| |的值等于________.
|的值等于________.
[提示]由 与
与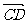 共线,先得x =10,再求|
共线,先得x =10,再求| |的长.
|的长.
[答案] .
.
[点评]本题考查向量的模、向量的坐标运算及向量共线的充要条件.
1.已知向量 =(1,2),
=(1,2), =(3,1),那么向量2
=(3,1),那么向量2 -
-
 的坐标是_________.
的坐标是_________.
[提示]
2 -
-

=2(1,2)- (3,1)
(3,1)
=(2,4)-(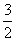 ,
, )
)
=(2-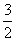 ,4-
,4- )
)
=( ,3
,3 ).
).
[答案]( ,3
,3 ).
).
[点评]本题考查平面向量的坐标运算.
6.如图,D、C、B三点在地面同一条直线上,从C、D两点测得A点仰角分别为a、b,
(a >b),则A点距地面高度AB等于( ).
(A)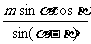 (B)
(B)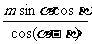
(C)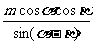 (D)
(D)
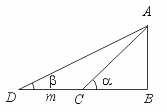
[提示]在△ACD由正弦定理,得AC = ,再在直角三角形中求AB.
,再在直角三角形中求AB.
[答案](A).
[点评]本题主要考查应用正弦定理解三角形的有关知识.
5.设s、t为非零实数, 与
与 均为单位向量时,若|s
均为单位向量时,若|s +t
+t |=|t
|=|t -s
-s |,则
|,则 与
与 的夹角q 的大小为( ).
的夹角q 的大小为( ).
(A)30° (B)45° (C)60° (D)90°
[提示]
由|s +t
+t |=|t
|=|t -s
-s |,得s2
|,得s2 2+t2
2+t2 2+2 st
2+2 st ·
·  =t2
=t2 2+s2
2+s2 2-2 st
2-2 st
 .
.
又 、
、 均为单位向量,|
均为单位向量,| |=1,|
|=1,| |=1,
|=1,
即 2=1,
2=1, 2=1.
2=1.
∴ 4 s
t  ·
· =0,有|
=0,有| |·|
|·| |cos q =0,得cos q =0.
|cos q =0,得cos q =0.
∴ q =90°.
[答案](D).
[点评]本题主要考查平面向量的数量积及运算律.
4.平面上有三个点A(1,3),B(2,2),C(7,x),若∠ABC =90°,则x的值为( ).
(A)5 (B)6 (C)7 (D)8
[提示]
∠ABC =90°,即 ⊥
⊥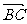 ,因
,因 =(1,-1),
=(1,-1),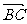 =(5,x -2),得1×5+(-1)×(x -2)=0,解出x =7.
=(5,x -2),得1×5+(-1)×(x -2)=0,解出x =7.
[答案](C).
[点评]本题考查向量的坐标运算及向量垂直的充要条件.
3.下列各组向量中,共线的是( ).
(A) =(-2,3),
=(-2,3), =(4,6)
=(4,6)
(B) =(1,-2),
=(1,-2), =(7,14)
=(7,14)
(C) =(2,3),
=(2,3), =(3,2)
=(3,2)
(D) =(-3,2),
=(-3,2), =(6,-4)
=(6,-4)
[提示]若 =(x,y),
=(x,y), =(x2,y2),则
=(x2,y2),则 与
与 共线的充要条件是x1 y2-x2 y1 =0.这里(-3)×(-4)-2×6=0.故选(D).
共线的充要条件是x1 y2-x2 y1 =0.这里(-3)×(-4)-2×6=0.故选(D).
[答案](D).
[点评]
本题以坐标的形式考查向量共线的充要条件.
对于(A),(-2)×6-3×4=-24≠0,排除(A);
对于(B),1×14-(-2)×7=28≠0,排除(B);
对于(C),2×2-3×3=-5≠0,排除(C).
2.若向量 =(3,2),
=(3,2), =(0,-1),则向量2
=(0,-1),则向量2 -
- 的坐标是( ).
的坐标是( ).
(A)(3,-4) (B)(-3,4) (C)(3,4) (D)(-3,-4)
[提示]2 -
- =2(0,-1)-(3,2)=(-3,-4).
=2(0,-1)-(3,2)=(-3,-4).
[答案](D).
[点评]本题考查向量的坐标运算.
1.计算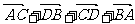 等于( ).
等于( ).
(A)0 (B)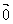 (C)2
(C)2 (D)2
(D)2 
[提示]
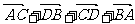 =(
=(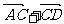 )+(
)+( )=
)= =
=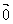 .
.
[答案](B).
[点评]本题考查向量的加法及运算律,相反向量,零向量的表示方法.
4.试证:从任意五个向量中总可以选出两个,使得它们之和的长不超过其余三个向量之和的长.
[提示]
这是一个存在性命题,由于五个向量是任意、故很难从正向直接推证,可采用反证法.
[证明]
考虑五个向量 ,
,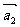 ,
,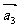 ,
,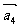 ,
,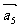 ,假设其中任意两个向量和的长均大于其余三个向量和之长,则有
,假设其中任意两个向量和的长均大于其余三个向量和之长,则有
| +
+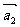 |>|
|>|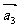 +
+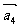 +
+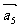 |,
|,
∴ | |2+2
|2+2 ·
·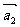 +|
+|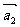 |2>|
|2>|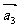 |2+|
|2+|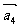 |2+|
|2+|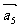 |2+2(
|2+2(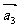 ·
·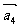 )+2
)+2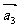 ·
·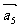 +2
+2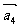 ·
·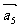 .
.
这里类似上面的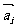 +
+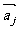 (i ≠j).共有10种情况,这10个不等式,左边、右边分别相加,得
(i ≠j).共有10种情况,这10个不等式,左边、右边分别相加,得
4(| |2+|
|2+|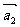 |2+…+|
|2+…+|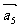 |2)+2
|2)+2
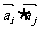 >6(|
>6(| |2+|
|2+|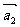 |2+…+|
|2+…+|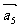 |2)+6
|2)+6
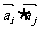 .
.
整理值有 | +
+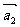 +
+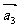 +
+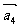 +
+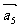 |2<0.
|2<0.
这是不可能的,故假设不真,原命题得证.
[点评]
本题就知识而言重点考查向量的数量积运算:就方法而言考查了反证法的数学方法.就能力而言考查了思维能力及严密的推理论证能力.题目所证虽然是存在性问题,能从五个向量中,找到一种情况即可.但由于已知向量的任意性,使得情况变的复杂,逐一排除进行挑选确定难度很大,运用等价命题的思想采用反证法十分凑效.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com