
题目列表(包括答案和解析)
2. 掌握对数函数的概念,并能求出对数函数的定义域和值域。
第五单元 对数与对数函数
[重点难点]
1. 理解对数的概念,能够进行对数式与指数式的互化;掌握对数的运算性质,能够熟练应用对数运算性质进行计算或证明;了解常用对数和自然对数的概念。
4.已知平面向量 =(7,9),若向量
=(7,9),若向量 、
、 满足2
满足2 +
+ =
= ,
, ⊥
⊥ ,|
,| |=|
|=| |,求
|,求 、
、 的坐标.
的坐标.
[提示]
设 =(x1,x2),
=(x1,x2), =(y1,y2),由已知,可以得到含有x1,x2,y1,y2的四个关系式,建立方程组,解之即可.
=(y1,y2),由已知,可以得到含有x1,x2,y1,y2的四个关系式,建立方程组,解之即可.
[答案]
设 =(x1,x2),
=(x1,x2), =(y1,y2).
=(y1,y2).
由2 +
+ =
= ,得
,得
2(x1,x2)+(y1,y2)=(7,9),
即
由 ⊥
⊥ ,得x1y1+x2y2=0. ③
,得x1y1+x2y2=0. ③
由 | |=|
|=| |,得 x12+x22=y12+y22=0. ④
|,得 x12+x22=y12+y22=0. ④
将(1)式化为 y1=7-2 x1,
(2)式化为 y2=9-2 x2,
代入③式,得 x1(7-2 x1)+x2(9-2 x2)=0,
即 2(x12+x22)=7 x1+9 x2, ⑤
代入④式,得 x12+x22=(7-2 x1) 2 +(9-2 x2) 2,
即 3(x12+x22)=28 x1+36 x2-130. ⑥
由⑤、⑥,得

解之得, 或
或
分别代入(1)、(2),得
 或
或
∴  =(
=( ,
,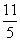 ),
), =(-
=(-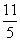 ,
, ).
).
或  =(1,5),
=(1,5), =(5,-1)即为所求.
=(5,-1)即为所求.
[点评]
本题考查向量的坐标运算,向量垂直的充要条件,两点间距离公式及运算能力.
3.如图,某观测站C在城A的南偏西20°方向上,从城A出发有一条出路,走向是南偏东40°,在C处测得距C处31千米的公路上的B处有一人正沿着公路向城A走去.走20千米后到达D处.测得CD =21千米,这时此人距城A多少千米.

[提示]
要求AD的长,在△ACD中,应用正弦定理,只需求∠ACD,而∠CDB是△ACD的一个外角,∠CAD已知,故只需求∠CDB,在△CDB中,已知两边,可利用余弦定理求角.
[答案]
由已知,在△CDB中,CD =21,DB =20,BC =31,据余弦定理,有
cos ∠CDB =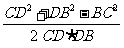 =-
=- .
.
∴ sin ∠CDB = =
= .
.
在△ACD中,∠CAD =20°+40°=60°,
∴ ∠ACD =∠CDB -∠CAD =∠CDB -60°.
∴ sin ∠ACD =sin(∠CDB -60°)
=sin ∠CDB cos 60°-cos ∠CDB sin 60°
= ×
× -(-
-(- )×
)×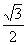
=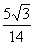 .
.
由正弦定理,得
AD = · sin ∠ACD =15(千米).
· sin ∠ACD =15(千米).
答:此人距A城15千米.
[点评]
本题结合三角函数的知识,主要考查了正弦、余弦定理的应用.解此类应用问题的关键是正确理解题意,建立数学模型,将实际问题转化为解斜三角形的问题,再根据正弦、余弦定理予以解决.
4.在□ABCD中,对角线AC =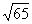 ,BD =
,BD =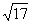 ,周长为18,求这个平行四边形的面积.
,周长为18,求这个平行四边形的面积.
[提示一]
要求得平行四边形的面积,须知两条邻边及它的夹角.由周长为18,知两条邻边的和为9,可据两条已知的对角线,利用余弦定理求得两条邻边及夹角.
[提示二]在△AOB和△BOC中利用余弦定理求解.

[解法一]如图,在□ABCD中,设AB =x,则BC =9-x,
在△ABC中,据余弦定理,得
AC2=AB2+BC2-2 AB BC cos ABC.
在△ABD中,据余弦定理,得
BD2=AB2+AD2-2 AB · AD cos DAB.
由已知 AC
=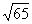 ,BD =
,BD =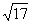 ,∠DAB +∠ABC =180°,BC =AD.
,∠DAB +∠ABC =180°,BC =AD.
故角 65=x 2 +(9-x) 2 -2 AB BC cos ABC,
17=x 2 +(9-x 2)+2 AB BC cos ABC,
二式相加,得
82=4 x2-36 x +162
即 x2-9 x +20=0
解得 x =4,或x =5,
在△ADB中,由余弦定理,得
cos ∠DAB =
=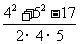
= .
.
∴ sin
∠DAB =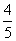 .
.
∴ sin □ABCD =AB · AD sin DAB
=4×5×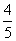
=16.
[解法二]在△AOB和△BOC中,由余弦定理,得
AB2=OA2+OB2-2 OA · OB cos ∠AOB,
BC2=OC2+OB2-2 OC · OB cos ∠BOC,
可设 AB =x,则BC =9-x,
而OA =OC = AC,OB =
AC,OB = BD,∠AOB +∠BOC =180°,
BD,∠AOB +∠BOC =180°,
代入后化简,可求得
x =4或x =5.
在△ADB中,由余弦定理,得
cos ∠DAB =
=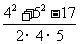
= .
.
∴ sin
∠DAB =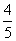 .
.
∴ sin □ABCD =AB · AD sin DAB
=4×5×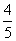
=16.
[点评]本题考查余弦定理的灵活运用.
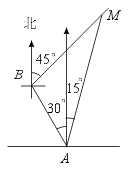
3.一只船按照北偏西30°方向,以36海里/小时的速度航行,一灯塔M在船北偏东15°,经40分钟后,灯塔在船北偏东45°.求船与灯塔原来的距离.
[提示]
先画船航行的示意图,将题目的已知条件分别与三角形内的边、角对应起来,从而确定三角形内的边角关系,运用正弦定理或余弦定理解决.
[答案]
如图,设船原来的位置为A,40分钟后的位置为B,则AB =36× =24(海里).
=24(海里).
在△ABM中,∠BAM =30°+15°=45°.
∠ABM =180°-(45°+30°)=105°,
∴ ∠AMB =180°-(∠ABM +∠BAM)=30°.
由正弦定理,得
AM = · sin ∠ABM
· sin ∠ABM
= · sin 105°
· sin 105°
=12(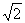 +
+ )(海里).
)(海里).
答:船与灯塔原来的距离为12(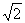 +
+ )海里.
)海里.
[点评]
本题考查解斜三角形的应用问题.关键是画出示意图(这里必须弄清方位角的概念),建立数学模型,将实际问题转化为解斜三角形的问题.
2.如图,已知 =
= =
= ,
,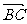 =
= ,且|
,且| |=|
|=| |.
|.
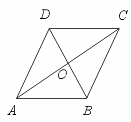
(1)用 ,
, 表示
表示 ,
,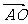 ,
,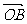 ;
;
(2)求 ·
· .
.
[提示]
由 =
= ,可判定四边形ABCD为平行四边形,于是利用平行四边形的性质.可求
,可判定四边形ABCD为平行四边形,于是利用平行四边形的性质.可求 ,
,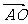 ,
,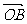 .又
.又 =
= +
+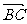 .
. =
= -
- ,
, =
=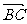 利用数量积的运算性质及已知条件|
利用数量积的运算性质及已知条件| |=|
|=| |.可求
|.可求 ·
· .
.
[答案]
(1)∵  =
= ,
,
∴ 四边形ABCD为平行四边形.
∴  =
=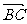 =
= .
.
∴  =
= +
+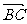 =
= +
+ ,
, =
= -
- =
= -
- ,
,
而 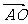 =
=
 ,
,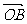 =-
=-
 ,
,
∴ 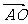 =
=
 +
+
 ,
,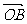 =
=
 -
-
 .
.
(2)∵  =
= +
+ ,
, =
= -
- ,
,
∴  ·
· =(
=( +
+ )(
)( -
- )
)
= 2-
2- 2
2
=| |2-|
|2-| |2
|2
=0.
[点评]
本题考查平面向量的加减法,基本定理、数量积及运算律.解题时注意结合平面图形的几何特征,寻求向量之间的联系.由题目的条件及结论可知,四边形ABCD为菱形.
1.设平面三点A(1,0),B(0,1),C(2,5).
(1)试求向量2 +
+ 的模;
的模;
(2)试求向量 与
与 的夹角;
的夹角;
(3)试求与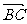 垂直的单位向量的坐标.
垂直的单位向量的坐标.
[提示]
 、
、 的坐标为终点坐标与始点坐标的差,求出
的坐标为终点坐标与始点坐标的差,求出 、
、 的坐标后,可得2
的坐标后,可得2 +
+ 的坐标,(1)可解,对于(2),可先求
的坐标,(1)可解,对于(2),可先求 、
、 的值,代入 cos q =
的值,代入 cos q = ,即可;对于(3),设所求向量的坐标为(x,y),根据题意,可得关于x、y的二元方程组,解出x,y.
,即可;对于(3),设所求向量的坐标为(x,y),根据题意,可得关于x、y的二元方程组,解出x,y.
[答案]
(1)∵  =(0-1,1-0)=(-1,1),
=(0-1,1-0)=(-1,1),
 =(2-1,5-0)=(1,5).
=(2-1,5-0)=(1,5).
∴ 2 +
+ =2(-1,1)+(1,5)=(-1,7).
=2(-1,1)+(1,5)=(-1,7).
∴ |2 +
+ |=
|= =
= .
.
(2)∵ | |=
|=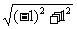 =
=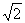 .
.
| |=
|= =
= ,
,
 ·
· =(-1)×1+1×5=4.
=(-1)×1+1×5=4.
∴ cos q = =
=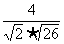 =
=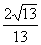 .
.
(3)设所求向量为 =(x,y),则
=(x,y),则
x2+y2=1. ①
又 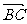 =(2-0,5-1)=(2,4),由
=(2-0,5-1)=(2,4),由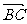 ⊥
⊥ ,得
,得
2 x +4 y =0. ②
由①、②,得 或
或
∴ (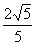 ,-
,-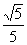 )或(-
)或(-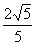 ,
,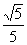 )即为所求.
)即为所求.
[点评]
本题考查向量的模,向量的坐标运算、向量的数量积,向量垂直的充要条件以及运算能力.
5.在△ABC中,已知a =2,b =2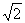 ,c =
,c = +
+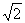 .则这个三角形的最小角的度数是___________.
.则这个三角形的最小角的度数是___________.
[提示]
先由已知条件判断△ABC三条边中的最短的边,它所对的角便是该三角形的最小角.由于c >b >a,则a对的角A为最小.利用余弦定理,得
cos A =
=
=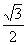 ,
,
∴ A =30°.
[答案]30°.
[点评]本题主要考查应用余弦定理解决三角形的有关问题.
4.将点A(2,4)按向量 =(-5,-2)平移后,所得到的对应点A′的坐标是______.
=(-5,-2)平移后,所得到的对应点A′的坐标是______.
[提示]由已知,x =2,y =4,h =-5,k =-2,代入平移公式 ,得x′=-3,y′=2.
,得x′=-3,y′=2.
[答案](-3,2).
[点评]本题考查点的平移公式.主要应分清平移前后点的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com