
题目列表(包括答案和解析)
2.若f(cos x)=cos 2x,则f(sin 15°)的值是( ).
(A) (B)
(B) (C)-
(C)- (D)-
(D)-
[提示一]
由f(cos x)=cos 2x=2 cos2 x-1,得f(x)=2x2-1,于是
f(sin 15°)=2 (sin 15°)2-1=―cos30°=― .
.
[提示二]
f(sin 15°)=f(cos 75°)=cos 150°=―cos30°=― .
.
[答案](D).
[点评]本题结合函数的概念考查二倍角公式或诱导公式的灵活应用.
1.下列命题中,真命题是( ).
(A)若sin a>0,则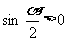
(B)若sin a>0,则cos a>0
(C)若tan a>0,则sin 2a >0
(D)若cos a <0,则cos 2a<0
[提示]根据三角函数值的符号,确定角a 所在的象限,再由角 ,2 a 所在的象限,判断相应三角函数值的符号.
,2 a 所在的象限,判断相应三角函数值的符号.
[答案](C).
[点评]
本题考查三角函值的符号.由sin a >0,得2kp<a
<2kp+p(k Z),于是
Z),于是
kp< <kp+
<kp+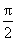 (k
(k Z),知
Z),知 是第一或第三象限角,故排除(A).
是第一或第三象限角,故排除(A).
由sin a>0,得a 是第一或第二象限角,排除(B).
由cos a <0,得2kp+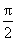 <a <2kp+
<a <2kp+ (k
(k Z),于是4kp+p<2a <4kp+3p (k
Z),于是4kp+p<2a <4kp+3p (k Z),此时,2a
可能是任何象限的角,排除(D).
Z),此时,2a
可能是任何象限的角,排除(D).
而由tan a>0,知kp<a <kp+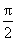 (k
(k Z),于是2kp<2a <2kp+p,此时sin 2a >0成立.
Z),于是2kp<2a <2kp+p,此时sin 2a >0成立.
8.由已知x= -2y>0,
-2y>0, ,由g=log
,由g=log
 (8xy+4y2+1)=log
(8xy+4y2+1)=log (-12y2+4y+1)=log
(-12y2+4y+1)=log [-12(y-
[-12(y- )2+
)2+ ],
], 当y=
当y= ,g的最小值为log
,g的最小值为log

7.由y=log3 ,得3y=
,得3y= ,即(3y-m)x2-8x+3y-n=0. ∵x
,即(3y-m)x2-8x+3y-n=0. ∵x -4(3y-m)(3y-n)
-4(3y-m)(3y-n) 0,即32y-(m+n)·3y+mn-16
0,即32y-(m+n)·3y+mn-16 。由0
。由0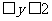 ,得
,得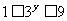
,由根与系数的关系得 ,解得m=n=5。
,解得m=n=5。
6.∵
 -
- 。
。
5.(1)∵f(x2-3)=lg ,∴f(x)=lg
,∴f(x)=lg ,又由
,又由 得x2-3>3,∴ f(x)的定义域为(3,+
得x2-3>3,∴ f(x)的定义域为(3,+ )。
)。
(2)∵f(x)的定义域不关于原点对称,∴ f(x)为非奇非偶函数。
(3)由y=lg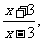 得x=
得x= ,
, x>3,解得y>0, ∴f-1(x)=
x>3,解得y>0, ∴f-1(x)=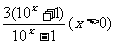
(4) ∵f[ ]=lg
]=lg ,∴
,∴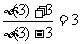 ,解得
,解得 (3)=6。
(3)=6。
3. 由2(log2x)2-7log2x+3 0解得
0解得
 log2x
log2x 3。∵f(x)=log2
3。∵f(x)=log2 (log2x-2)=(log2x-
(log2x-2)=(log2x- )2-
)2- ,∴当log2x=
,∴当log2x= 时,f(x)取得最小值-
时,f(x)取得最小值- ;当log2x=3时,f(x)取得最大值2。
;当log2x=3时,f(x)取得最大值2。
3.(1)f(x)= ,
,
,且x1<x2,f(x1)-f(x2)= <0,(∵102x1
<0,(∵102x1 <102x2)∴f(x)为增函数。
<102x2)∴f(x)为增函数。
(2)由y= 得102x=
得102x=
∵102x>0,
∴-1<y<1,又x= )。
)。
2. 已知f(x)=lg
 ①,又∵f(
①,又∵f(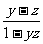 )=lg
)=lg ②,
②,
①②联立解得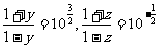 ,∴f(y)=
,∴f(y)= ,f(z)=-
,f(z)=- 。
。
1. f(x)-g(x)=logx3x-logx4=logx .当0<x<1时,f(x)>g(x);当x=
.当0<x<1时,f(x)>g(x);当x= 时,f(x)=g(x);当1<x<
时,f(x)=g(x);当1<x< 时,f(x)<g(x);当x>
时,f(x)<g(x);当x> 时,f(x)>g(x)。
时,f(x)>g(x)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com