
题目列表(包括答案和解析)
2.求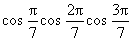 的值等于________.
的值等于________.
[提示]
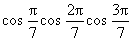
=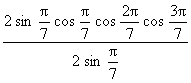
=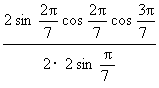
=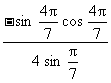
=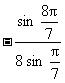
=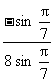 =
= .
.
[答案] .
.
[点评]本题考查二倍角公式及诱导公式以及三角恒等变形的能力.
1.函数y=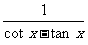 的周期T =_______.
的周期T =_______.
[提示一]
y=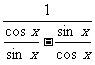
=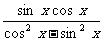
=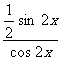 =
= tan 2x.
tan 2x.
[提示二]
y=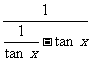
=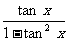
= tan 2 x.
tan 2 x.
[答案]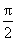
[点评]本题考查同角三角函数关系,二倍角公式及正切函数的周期性.
10.已知tan a ,tan b 是方程x2+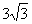 x+4=0的两根,且-
x+4=0的两根,且-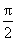 <a
<
<a
<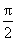 ,-
,-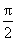 <b
<
<b
<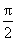 ,则a
+b 等于( ).
,则a
+b 等于( ).
(A)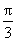 (B)-
(B)-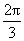 (C)
(C)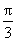 或
或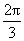 (D)-
(D)-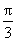 或
或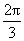
[提示]
因为tan a +tan b =-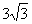 ,tan a tan b =4,则tan(a+b )=
,tan a tan b =4,则tan(a+b )= =
=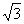 .同时由tan a +tan b
<0,tan a tan b
>0,可知tan a ,tan b
均小于零, 故a 、b
.同时由tan a +tan b
<0,tan a tan b
>0,可知tan a ,tan b
均小于零, 故a 、b
 (-
(-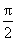 ,0),所以a +b
,0),所以a +b
 (-p ,0),得a +b =-
(-p ,0),得a +b =-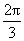 .
.
[答案](B).
[点评]本题考查两角和的正切公式,以及综合运用韦达定理解决问题的能力.
9.使函数y=sin(2x+q )+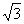 cos(2x+q )为奇函数,且在[0,
cos(2x+q )为奇函数,且在[0,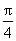 ]上是减函数的q 的一个值是( ).
]上是减函数的q 的一个值是( ).
(A)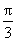 (B)
(B)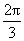 (C)
(C)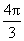 (D)
(D)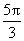
[提示]
由于y=2 sin(2x+q
+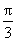 )为奇函数,再将各选项的q 的值逐项代入,可排除(A)、(C).又x∈[0,
)为奇函数,再将各选项的q 的值逐项代入,可排除(A)、(C).又x∈[0,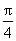 ] 时原函数为减函数,再排除(D).
] 时原函数为减函数,再排除(D).
[答案](B).
[点评]本题考查两角和的正弦公式、函数的奇偶性以及函数的单调性.
8.下列各式中正确的是( ).
(A)arcsin(-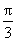 )=-
)=-
(B)arcsin(sin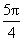 )=-
)=-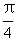
(C)arcsin(arcsin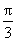 )=
)=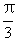
(D)sin[arccos(- )]=-
)]=-
[提示]利用反正弦函数、反余弦函数的定义.
[答案](B).
[点评]本题考查反正弦、反余弦的定义.对于arcsin x=a ,x表示角a的正弦值,且| x | 1,而-
1,而-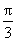 <-1,排除(A);又
<-1,排除(A);又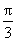 >1,排除(C);由于arccos(-
>1,排除(C);由于arccos(- )=
)=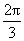 ,sin
,sin 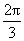 =
= ,排除(D).而sin
,排除(D).而sin 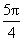 =-
=-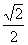 ,arcsin(-
,arcsin(-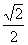 )=-
)=-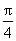 .故选(B).
.故选(B).
7.函数y=A sin(w x+j)在同一区间内,当x= 时,y取得最大值
时,y取得最大值 ;当x=
;当x= 时,y取得最小值-
时,y取得最小值- ,则函数的解析式是( ).
,则函数的解析式是( ).
(A)y= sin(
sin(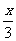 -
-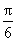 )
)
(B)y= sin(3x+
sin(3x+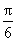 )
)
(C)y= sin(
sin(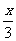 +
+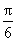 )
)
(D)y= sin(3x-
sin(3x-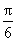 )
)
[提示]
显然A= ,
, =
= -
-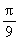 =
=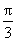 ,T =
,T =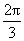 .则w
=
.则w
= =3,将(
=3,将( ,
, )代入
)代入
y= sin(3x+j),得j =
sin(3x+j),得j =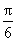 ,于是y=
,于是y= sin(3x+
sin(3x+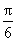 ).
).
[答案](B).
[点评]本题考查三角函数y= A sin(w x+j)的图象和性质.
6.在直角三角形中两锐角为A和B,则sin A sin B( ).
(A)有最大值 和最小值0
和最小值0
(B)有最大值 ,但无最小值
,但无最小值
(C)既无最大值也无最小值
(D)有最大值1,但无最小值
[提示]
因为A+B=90°,有sin A sin B=sin A cos A= sin 2A.又0°<A<90°,所以当
sin 2A.又0°<A<90°,所以当
A=45°时,sin A sin B有最大值 ,但2A∈(0,180°),sin 2A无最小值.
,但2A∈(0,180°),sin 2A无最小值.
[答案](B).
[点评]本题考查三角函数的诱导公式及二倍角的正弦公式、正弦函数的有界性等知识.
5.要使sin a -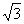 cos a =
cos a =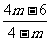 有意义,m的取值范围是( ).
有意义,m的取值范围是( ).
(A)[-1,0] (B)[0,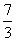 ] (C)[-1,
] (C)[-1,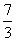 ] (D)[
] (D)[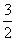 ,4]
,4]
[提示]
由于sin a -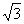 cos a =2sin(a -
cos a =2sin(a -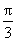 ),得-2
),得-2
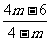
 2 ,解不等式,得
2 ,解不等式,得
m∈[-1,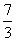 ].
].
[答案](C).
[点评]本题考查两角差的正弦,三角函数的值域以及解不等式的有关知识.
4.比较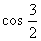 ,
,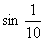 ,-
,- 的大小顺序是( ).
的大小顺序是( ).
(A)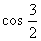 <
<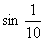 <-
<-
(B)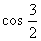 <-
<- <
<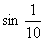
(C)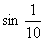 <
<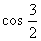 <-
<-
(D)- <
<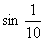 <
<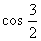
[提示]
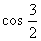
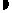 cos 86°,
cos 86°,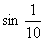
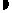 sin 5.7°=cos 84.3°,-
sin 5.7°=cos 84.3°,-
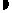 -cos100.3°=cos 79.7°,而y=cos x在(0,
-cos100.3°=cos 79.7°,而y=cos x在(0,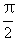 )为减函数,得
)为减函数,得
cos 86°<cos 84.3°<cos 79.7°,即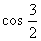 <
<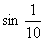 <-
<- .
.
[答案](A).
[点评]本题考查诱导公式及余弦函数的单调性.在比较大小时,一般是先将各三角函数都化为同名的三角函数,再将各角化为第一象限的角,最后利用三角函数的单调性来比较.
3.下列函数中,周期为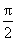 的偶函数是( ).
的偶函数是( ).
(A)f(x)=sin 4x,x∈R
(B)f(x)=cos2 2x-sin2 2x, x∈R
(C)f(x)=tan 2x,x∈R且x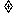
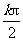 +
+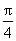 (k∈Z)
(k∈Z)
(D)f(x)=cos 2x,x∈R
[提示]
(A)、(C)中的函数为奇函数,(D)中的函数周期是p
,而对于(B),f(x)=cos 4x 是周期为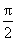 的偶函数.
的偶函数.
[答案](B).
[点评]本题考查三角函数的奇偶性、周期性和二倍角公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com