
题目列表(包括答案和解析)
2.函数f(x)=M sin(wx+j)(w >0)在区间[a,b]上是增函数,且f(a)=-M,
f(b)=M,则函数g(x)=M cos(w x+j)在[a,b]上( ).
(A)是增函数
(B)是减函数
(C)可以取得最大值M
(D)可以取得最小值-M
[提示]
利用特殊值法,令M=w =1,j
=0,则有 f(x)=sin x,g(x)=cos x,同时a=-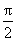 ,b=
,b=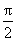 ,可见,g(x)在[a,b](即[-
,可见,g(x)在[a,b](即[-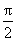 ,
,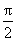 ])上既不是增函数,也不是减函数,但可以取得最大值1,故排除(A)、(B)、(D).本题也可以用作图法求解.
])上既不是增函数,也不是减函数,但可以取得最大值1,故排除(A)、(B)、(D).本题也可以用作图法求解.
[答案](C).
[点评]本题考查正弦函数、余弦函数的性质以及灵活运用这些知识解决问题的能力.
1.“a=1”是“函数y=cos2 ax-sin2 ax的最小正周期为 p ”的( ).
(A)充分而不必要条件
(B)必要而不充分条件
(C)充要条件
(D)既不充分也不必要条件
[提示]
由于y=cos2 ax-sin2 ax=cos 2ax,当a=1时,函数的最小正周期为p ,当a=-1时,函数的最小正周期也是p ,所以 a=1是函数的最小正周期为p 的充分而不必要条件.
[答案](A).
[点评]本题考查倍角公式和三角函数的周期性以及充要条件的知识.
5.设函数y=sin 2
x+a cos x+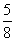 a-
a-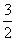 在0
在0 x
x
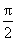 上的最大值为1,求a的值.
上的最大值为1,求a的值.
[提示]
将函数y变形为y=-(cos x-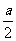 )2+
)2+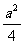 +
+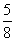 a-
a- ,由cos x
,由cos x  [0,1],利用二次函数的图象性质,分情况讨论.
[0,1],利用二次函数的图象性质,分情况讨论.
[答案]
∵ y=sin 2
x+a cos x+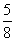 a-
a-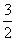
=1-cos 2 x+a cos x+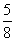 a-
a-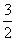
=-(cos x-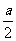 )2+
)2+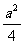 +
+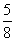 a-
a- .
.
由0 x
x
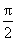 ,得0
,得0 cos x
cos x 1.
1.
下面对a的取值情况分类讨论:
(1)当0 a
a 2时,函数y在cos x=
2时,函数y在cos x=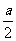 处取得最大值
处取得最大值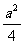 +
+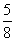 a-
a- ,据已知,
,据已知,
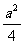 +
+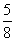 a-
a- =1,即2a2+5a-12=0,得a=
=1,即2a2+5a-12=0,得a=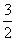 或a=-4(舍去);
或a=-4(舍去);
(2)当a<0时,函数y在cos x=0时取得最大值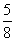 a -
a - ,有
,有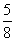 a -
a - =1,
=1,
即a=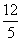 (舍去);
(舍去);
(3)当a>2时,函数y在cos x=1处取得最大值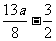 ,有
,有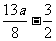 =1,
=1,
即a =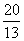 (舍去).
(舍去).
∴ a =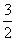 即为所求.
即为所求.
[点评]本题通过三角函数的有界性,结合二次函数的性质考查在限定区间内函数的最大(小)值的问题,以及综合运用数学知识解决问题的能力.
4.已知函数y=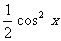 +
+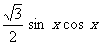 +1,x
+1,x R
R
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图象可由y=sin x,x R的图象经过怎样的平移和伸缩变换得到?
R的图象经过怎样的平移和伸缩变换得到?
[提示]利用三角函数的有关公式,对函数y进行化简.
[答案] (1)y=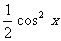 +
+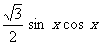 +1
+1
=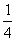 (2 cos2 x-1)+
(2 cos2 x-1)+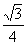 (2 sin x cos x)+
(2 sin x cos x)+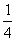 +1
+1
=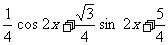
=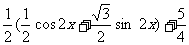
=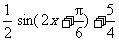 .
.
当y取最大值时,必须有2x+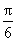 =2kp+
=2kp+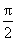 ,即x=kp+
,即x=kp+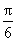 (k
(k Z).
Z).
∴ 当函数y取得最大值时,自变量x的集合为 x {x=kp+
{x=kp+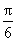 ,k
,k Z}.
Z}.
(2)[解法一]将函数y=sin x依次进行如下变换:
①把函数y=sin x的图象向左平行移动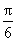 个单位长度,得到函数y=sin(x+
个单位长度,得到函数y=sin(x+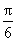 )的图象;
)的图象;
②把所得图象上各点的横坐标缩短到原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数
y=sin(2x+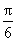 )的图象;
)的图象;
③把得到的图象上的各点的纵坐标缩短到原来的 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数
y=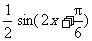 的图象;
的图象;
④把得到的图象向上平行移动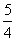 个单位长度,得到函数y=
个单位长度,得到函数y=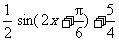 的图象.
的图象.
综上得到函数y=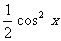 +
+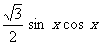 +1的图象.
+1的图象.
[解法二]
①把函数y=sin x图象上所有的点的横坐标缩短为原来的 倍(纵坐标不变),得到函数y=sin 2x的图象;
倍(纵坐标不变),得到函数y=sin 2x的图象;
②再将图象上所有的点向左平行移动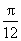 个单位长度,得函数y=
个单位长度,得函数y=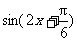 的图象;③将得到的图象上的所有点的纵坐标缩短为原来的
的图象;③将得到的图象上的所有点的纵坐标缩短为原来的 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数
y=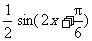 的图象;
的图象;
④将得到的图象向上平行移动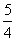 个单位长度,得函数y=
个单位长度,得函数y=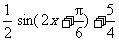 的图象.
的图象.
[点评]
本题是2000年高考题,主要考查三角函数的图象和性质,考查利用三角公式进行恒等变形的技能以及运算能力.注意:在由y=sin x的图象得到y=sin w x的图象时,是把y=sin x的图象上所有点的横坐标伸长(或缩短)到原来的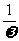 倍(纵坐标不变),而不是w
倍.
倍(纵坐标不变),而不是w
倍.
3.已知cos a =cos x·sin g ,cos b =sin x·sin g ,求证sin2 a +sin2 b +sin2 g =2
[提示] 利用已知条件,注意到sin2 a =1-cos2 a ,sin2 b =1-cos2 b ,将条件代入原式的左边,化简即可.
[答案]左边=1-cos2 a +1-cos2 b +sin2 g
=2-cos2 a -cos2 b +sin2 g ,
又cos a =cos x sin g ,cos b =sin x sin g ,
∴ 左边=2-cos2 x sin2 g -sin2 x sin2 g +sin2 g
=2-sin2 g(sin2 x+cos2 x)+sin2 g
=2-sin2 g+sin2 g
=2
∴ 原结论成立.
[点评]
本题通过三角恒等式的证明,考查三角函数恒等变形能力.寻求已知条件与所证恒等式之间的关系是证明的关键.
2.设p<A< ,0<B<
,0<B<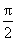 ,且cos A=-
,且cos A=-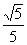 ,cot B=3,求证A-B=
,cot B=3,求证A-B=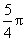 .
.
[提示]根据已知,先计算tan(A-B)的值,再判断A-B的取值范围.
[答案]∵ p<A< ,cos A=-
,cos A=-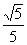 ,
,
∴ sin A=-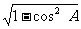 =
=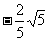 ,
,
于是,tan A=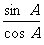 =2.
=2.
又cot B=3,得tan B= .
.
∴ tan(A-B)= =
=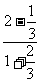 =1.
=1.
∵ p<A< ,0<B<
,0<B<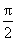 ,
,
∴ 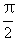 <A-B<
<A-B< .
.
∴ A-B=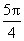 .
.
[点评]本题考查同角三角函数间的关系,两角差的正切,由三角函数值确定角的方法.
1.已知角a 的顶点与直角坐标系的原点重合,始边在x轴的非负半轴上,终边经过
点P(-1,2),求sin(2a +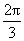 )的值.
)的值.
[提示]画出图形,先求得sin a ,cos a 的值.
[答案]据已知,| OP | =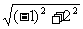 =
=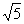 ,
,
由三角函数的定义,sin a =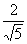 ,cos a =-
,cos a =-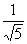 .
.
于是,sin 2a =2 sin a
cos a =-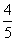 , cos 2a =2 cos2 a
-1=-
, cos 2a =2 cos2 a
-1=-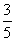 .
.
∴ sin(2a +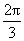 )=
)=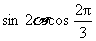 +
+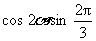
=-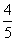 ×(-
×(- )+(-
)+(-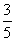 )×
)×
=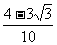 .
.
[点评]本题考查三角函数的定义,两角和的正弦、倍角公式及计算能力.
5.方程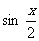 =
= 在[p,2p]上的解是___________.
在[p,2p]上的解是___________.
[提示]
由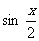 =
= ,得
,得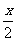 =kp+(-1)k
=kp+(-1)k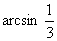 ,x=2kp+(-1)k
,x=2kp+(-1)k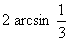 (k
(k Z),当k=1时,有x=2p-
Z),当k=1时,有x=2p-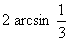
 [p,2p].
[p,2p].
[答案]2p-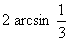 .
.
[点评]本题考查反正弦的定义.
4.函数f(x),x R是奇函数,且当x
R是奇函数,且当x 0时,f(x)=x2+sin x,则当x<0时,f(x)=____________.
0时,f(x)=x2+sin x,则当x<0时,f(x)=____________.
[提示]
当x<0时,-x>0,由题设f(-x)=(-x)2+sin(-x)=x2-sin x.,又f(x)为奇函数,f(-x)=-f(x),于是f(x)=-f(-x)=-x2+sin x.
[答案]-x2+sin x.
[点评]本题考查函数的概念,函数的奇偶性及运算能力.
3.函数y=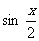 +
+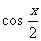 在(-2p,2p)内的递增区间是_____________.
在(-2p,2p)内的递增区间是_____________.
[提示]
y=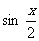 +
+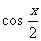 =
=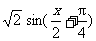 ,函数y的单调递增区间由下面的条件决定:
,函数y的单调递增区间由下面的条件决定:
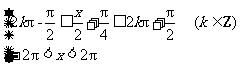
解之即可.
[答案][- ,
,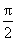 ].
].
[点评]本题考查三角函数式的恒等变形及三角函数的单调性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com