
题目列表(包括答案和解析)
2.函数y= 的值域为__________.
的值域为__________.
[提示一]化原函数为sin x= ,由|sin x|
,由|sin x| 1,得-1
1,得-1

 1,解之得-
1,解之得-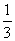
 y
y 1.
1.
[提示二]运用“分离常数法”.y= =-1+
=-1+ ,当sin x=-1时,函数的最小值为-
,当sin x=-1时,函数的最小值为-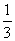 ;当x=1时,最大值为1.
;当x=1时,最大值为1.
[答案][-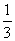 ,1].
,1].
[点评]本题考查三角函数的值域及其应用.
1.若角a 的顶点与原点重合,其始边与x轴的非负半轴重合,角a 的平分线过点(-p,p ),那么sin a =________,cos a =___________.
[提示]角a 的终边与y轴的非正半轴重合,即a = +2kp(k∈R).
+2kp(k∈R).
[答案]-1,0
[点评]本题考查三角函数的定义.
10.若0<a
< ,则arcsin[cos(
,则arcsin[cos( +a
)]+arccos[sin(p+a
)]等于( ).
+a
)]+arccos[sin(p+a
)]等于( ).
(A) (B)-
(B)- (C)
(C) -2a (D)-
-2a (D)- -2a
-2a
[提示] 用特殊值法,由0<a < ,取a
=
,取a
= ,
,
则原式=arcsin(- )+arccos(-
)+arccos(- )=-
)=- +
+ =
= .
.
[答案](A).
[点评]本题主要考查反正弦、反余弦的定义及解决问题的能力.
9.适合tan(2x+ )=
)= ,x∈
,x∈ 的x值的个数是( ).
的x值的个数是( ).
(A)2 (B)3 (C)4 (D)5
[提示]
由tan(2x+ )=
)= ,得2x+
,得2x+ =kp
+
=kp
+ (k∈Z),即x=
(k∈Z),即x= kp
-
kp
- (k∈Z),满足x∈
(k∈Z),满足x∈ 时,k可取1,2,3,4,故x的值为
时,k可取1,2,3,4,故x的值为 ,
, ,
, ,
,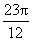 共4个值.
共4个值.
[答案](C).
[点评]本题考查反正切函数的定义.
8.要得到函数y=cos( -
- ),x∈R的图象,只需将函数y=
),x∈R的图象,只需将函数y=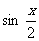 ,x∈R的图象( ).
,x∈R的图象( ).
(A)向左平行移动 个单位长度
个单位长度
(B)向右平行移动 个单位长度
个单位长度
(C)向左平行移动 个单位长度
个单位长度
(D)向右平行移动 个单位长度
个单位长度
[提示]
由y=cos( -
- )=cos(
)=cos( -
- )=
)= =
= =
=
[答案](A).
[点评]本题考查三角函数的图象和性质.注意:当由函数y= 的图象得到函数y=
的图象得到函数y=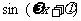 的图象时,需将函数y=
的图象时,需将函数y= 的图象上的所有点沿x轴平移
的图象上的所有点沿x轴平移 个单位长度(当
个单位长度(当 <0时向左移,当
<0时向左移,当 >0时向右移).
>0时向右移).
7.已知sin a
= ,a
,a  (
( ,p),tan(p-b)=
,p),tan(p-b)= ,则tan(a -2b )的值等于( ).
,则tan(a -2b )的值等于( ).
(A) (B)-
(B)- (C)
(C) (D)-
(D)-
[提示]
由sin a = ,a ∈(
,a ∈( ,p),得cos a =-
,p),得cos a =-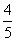 ,tan a =-
,tan a =- .
.
又tan(p-b)= ,得tan b =-
,得tan b =- ,tan 2b =
,tan 2b = =-
=- .
.
所以,tan(a -2b )=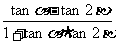 =
= .
.
[答案](A).
[点评]
本题考查同角三角函数的关系,诱导公式、二倍角的正切公式,两角差的正切公式以及运算能力.
6.已知f(x)= ,则当q
,则当q
 (
( ,
, )时,式子f(sin 2q )的值是( ).
)时,式子f(sin 2q )的值是( ).
(A)2 sin q (B)2 cos q (C)-2 sin q (D)-2 cos q
[提示]
f(sin 2q )-f(-sin 2q )
= -
-
= -
-
=|sin q -cos q |-|sin q +cos q |,
因为q  (
( ,
, ),得sin q <cos q <0,
),得sin q <cos q <0,
所以,原式=cos q -sin q+sin q +cos q =2 cos q .
[答案](B).
[点评]
本题考查函数的概念,三角函数值符号、二倍角公式以及三角函数恒等变形的能力.
5.设k是4的倍数加上1的自然数,若以cos x表示cos k x时,有cos k x=f(cos x),则sin k x等于( ).
(A)f(cos x) (B)f(sin x) (C)f(cos k x) (D)f(sin k x)
[提示]
由于sin a =cos( -a),设k=4n+1,(n=0,1,2,…),则有
-a),设k=4n+1,(n=0,1,2,…),则有
f(sin x)=f(cos( -a))=
-a))=
=
=cos[2np+ -(4n+1)x]
-(4n+1)x]
=cos[ -(4n+1)x]
-(4n+1)x]
=sin[(4n+1)x]
=sin k x .
以上各步均可逆.
[提示二]
利用特殊值法,令k=5,则f(cos x)=cos 5x sin 5x.排除(A),f(cos 5x)=
sin 5x.排除(A),f(cos 5x)=
cos(5×5x)=cos 25x sin 5x,排除(C),f(sin 5x)=f [cos(
sin 5x,排除(C),f(sin 5x)=f [cos( -5x)]=
-5x)]= =cos(
=cos( -25x)=sin 25x
-25x)=sin 25x sin 5x,排除(D),而f(sin x)=f [cos(
sin 5x,排除(D),而f(sin x)=f [cos( -x)]=
-x)]= =cos(
=cos( -5x)=sin 5x.
-5x)=sin 5x.
[答案](B).
[点评]本题考查函数的概念,诱导公式以及分析问题、解决问题的能力.
4.下列不等式中正确的是( ).
(A)e cos 52°<e cos 53°
(B)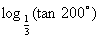 >
>
(C) >
>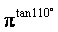
(D) <
<
[提示]利用函数的单调性.
[答案](A).
[点评]
本题综合指数函数、对数函数的性质考查三角函数的单调性.由于cos 52°>cos 53°,得ecos 52°>ecos 53°,排除(A);由于tan 200°=tan 20°,tan 199°=tan 19°,有
tan 20°>tan 19°,而0<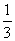 <1,得
<1,得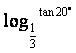 <
< ,排除(B);由于
,排除(B);由于
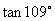 <
<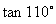 ,p >1,得
,p >1,得 <
< ,排除(C);而sin 115°>sin 116°,且0<
,排除(C);而sin 115°>sin 116°,且0<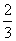 <1,有
<1,有 <
< .故选(D).
.故选(D).
3.已知a 、b 是锐角三角形的两个内角,则下列各式中成立的是( ).
(A)cos a >sin b ,cos b >sin a
(B)cos a <sin b ,cos b <sin a
(C)cos a >sin b ,cos b < sin a
(D)cos a <sin b ,cos b >sin a
[提示]
a 、b 是锐角三角形的两个内角,所以a +b >90°,a >90°-b ,故有
sin a >sin(90°-b),cos a <cos(90°-b),即sin a >cos b ,cos a <sin b.
[答案](B).
[点评]本题考查诱导公式以及正弦函数、余弦函数的单调性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com