
题目列表(包括答案和解析)
2.若a 是第四象限角,则p -a 是 ( ).
(A)第一象限角 (B)第二象限角
(C)第三象限角 (D)第四象限角
[提示]由a 是第四象限角,得-a 为第一象限角,p+(-a)为第三象限角.
[答案](C).
[点评]本题考查象限角之间的关系.
1.在下列各角中,第三象限角是( ).
(A)-540° (B)-150°
(C)-225° (D)510°
[提示]第三象限角a 满足180°+k ·360°<a <270°+k·360°,k∈Z.
[答案](B).
[点评]
本题考查终边相同的角的概念.与-540°终边相同的角为180°,为轴线角,故排除(A);与-225°终边相同的角为135°,为第二象限角,故排除(C);与510°终边相同的角为150°,也是第二象限角,排除(D).
5.记函数f (x) =1-2a-2acos x-2 sin2 x的最小值为f(a).
(1)写出函数f(a)的表达式;
(2)若f(a)=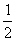 ,求这时函数f(a)的最大值.
,求这时函数f(a)的最大值.
[提示]
化简函数式,得f (x) =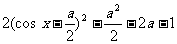 ,由| cos x |
,由| cos x |  1,利用二次函数的图象性质,应分情况讨论.
1,利用二次函数的图象性质,应分情况讨论.
[答案]
(1)∵ f (x) =1-2a-2a cos x-2 sin2 x
=1-2a-2a cos x-2(1-cos2 x)
=2 cos2 x-2a cos x-2a-1
=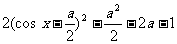 .
.
又 | cos x|  1,
1,
①当-1
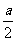
 1,即-2
1,即-2 a
a 2时,取cos x=
2时,取cos x=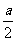 ,f(a)=
,f(a)=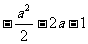 ;
;
②当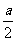 >1,即a>2时,取cos x=1,f(a)=
>1,即a>2时,取cos x=1,f(a)=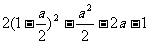 =1-4a;
=1-4a;
③当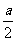 <-1,即a<-2 时,即cos x=-1,f(a)=
<-1,即a<-2 时,即cos x=-1,f(a)=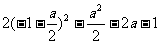 =1.
=1.
综上,有 f(a)=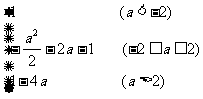 .
.
(2)若f(a)=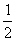 ,显然a
,显然a -2.
-2.
①当-2 a
a 2时,
2时,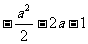 =
=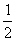 ,即a2 +4a+3=0,a=-1或a=-3(舍去),
,即a2 +4a+3=0,a=-1或a=-3(舍去),
②当a>2时,1-4a=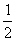 ,即a=
,即a=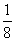 (舍去).
(舍去).
于是,满足f(a)=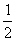 ,a=-1,此时,f(x)=
,a=-1,此时,f(x)=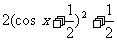 ,当cos a =1时,
,当cos a =1时,
f max(x)=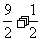 =5.
=5.
[点评]
本题综合二次函数的图象性质,考查与三角函数有关的函数最大(小)值的问题,考查灵活运用所学知识分析问题、解决问题的能力,以及数形结合、分类讨论、转化等数学思想方法.
4.已知sin 2a =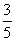 ,(-
,(-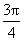 <a
<p ),函数f (x)=sin(a
-
x)-sin(a +x)+2 cos a 有最大值0 ,求当x为何值时,f (x)有最小值?最小值是多少?
<a
<p ),函数f (x)=sin(a
-
x)-sin(a +x)+2 cos a 有最大值0 ,求当x为何值时,f (x)有最小值?最小值是多少?
[提示]
化简函数式,得f (x)=2 cos a(1-sin x).根据题意,计算出cos a 的值,再利用
| sin x |  1,就可以求出f (x)的最小值.
1,就可以求出f (x)的最小值.
[答案]
∵ f (x)=sin(a -x)-sin(a +x)+2 cos a
=sin a cos x-cos a sin x-sin a cos x-cos a sin x+2 cos a
=2 cos a -2 cos a sin x
=2 cos a(1-sin x)
又f (x)≤0,
∴ 2 cos a(1-sin x)≤0,
而1-sin x≥0,
∴ cos a <0,
∵ -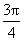 <a
<p ,
<a
<p ,
于是-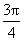 <a
<-
<a
<-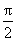 或
或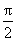 <a
<p,-
<a
<p,-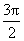 <2a <-p,或p <2a
<2p .
<2a <-p,或p <2a
<2p .
又sin 2a =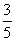 >0,
>0,
∴ -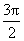 <2a <-p,且cos 2a =-
<2a <-p,且cos 2a =-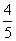 .
.
也就是2 cos 2 a =-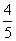 ,即cos a =-
,即cos a =-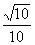 .
.
∴ f (x) =-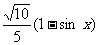 ,
,
当sin x=-1时,即x=2 kp-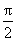 (k
(k Z)时,f (x)有最小值-
Z)时,f (x)有最小值-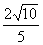 .
.
[点评]
本题综合考查三角函数的基础知识(两角和差的正弦公式、同角三角函数关系、二倍角公式、函数的最值等)以及运算能力.
3.已知△ABC的三个内角A、B、C满足A+C=2B,且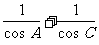 =
=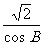 ,
,
求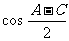 的值.
的值.
[提示]由题设A+C=2B,可得B=60°,考虑把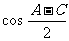 当作未知数,通过三角函数式的恒等变形,得到关于
当作未知数,通过三角函数式的恒等变形,得到关于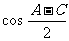 的一元二次方程解出
的一元二次方程解出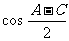 即可.
即可.
[答案]
∵ 在△ABC中,A+C=2B,
∴ B=60°,A+C=120°,
令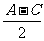 =q
,
=q
,
则由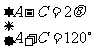 得
得 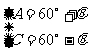
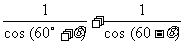
于是,
=
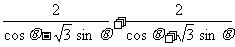
=
=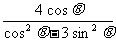
=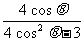
又 -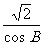 =-
=-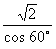 =-
=-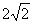 .
.
∵  =-
=-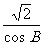 ,
,
∴ 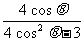 =-
=-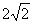 ,
,
即 =0 ,
=0 ,
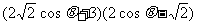 =0,
=0,
∵ 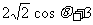
 0,
0,
∴ 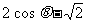 =0,cos q
=
=0,cos q
=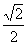 ,
,
所以,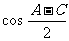 =
=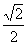 .
.
[点评]
本题综合考查三角函数的基础知识,考查灵活运用三角公式进行恒等变形运算的能力.
2.已知0<b
<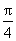 ,
,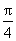 <a
<
<a
<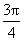 ,cos(
,cos(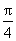 -a
)=
-a
)=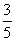 ,sin(
,sin(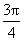 +b
)=
+b
)= ,
,
求sin(a +b )的值.
[提示]
用已知角表示所求角,注意到(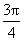 +b
)-(
+b
)-(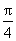 -a
)=
-a
)=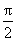 +(a
+b ),
+(a
+b ),
于是sin(a +b
)=-cos[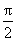 +(a
+b )]=-cos[(
+(a
+b )]=-cos[(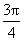 +b
)-(
+b
)-(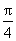 -a
)],
-a
)],
只要求出sin(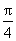 -a
),cos(
-a
),cos(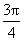 +b
)就可以了.
+b
)就可以了.
[答案]
∵ 0<b
<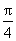 ,
,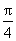 <a
<
<a
<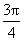 ,
,
∴ -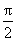 <
<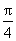 -a
<0,
-a
<0,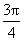 <
<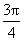 +b
<p.
+b
<p.
由cos(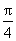 -a
)=
-a
)=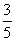 ,得sin(
,得sin(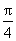 -a
)=-
-a
)=-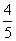 .
.
由sin(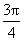 +b
)=
+b
)= ,得cos(
,得cos(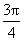 +b
)=-
+b
)=-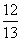 .
.
∴ sin(a
+b )=-cos[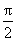 +(a
+b )]
+(a
+b )]
=-cos[(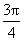 +b
)-(
+b
)-(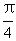 -a
)]
-a
)]
=- cos(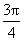 +b
)cos(
+b
)cos(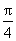 -a
)-sin(
-a
)-sin(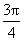 +b
)sin(
+b
)sin(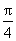 -a
)
-a
)
=―(―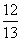 )×
)×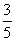 ―
― ×(―
×(―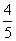 )
)
=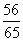
[点评]本题考查同角三角函数关系,诱导公式、两角差的余弦公式的灵活运用,考查计算推理能力以及变换的思想.
1.求值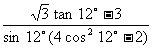 .
.
[提示]“切化弦”后,利用三角函数基础知识,可解.
[答案]
原式=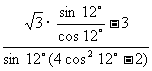
= 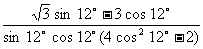
=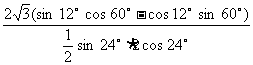
=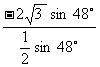
=-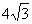
[点评]本题考查灵活运用同角三角函数关系、两角差的正弦、二倍角公式及运算能力.
5.函数y=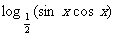 是减函数的区间为__________.
是减函数的区间为__________.
[提示]由y=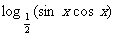 =
=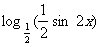 =1+
=1+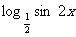 .
.
利用对数函数的定义域,知sin 2x>0,得x∈(kp ,kp+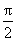 )(k∈Z).又y=sin 2x的递增区间为[-
)(k∈Z).又y=sin 2x的递增区间为[-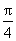 +kp ,
+kp ,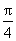 +kp](k∈Z),而y=sin 2x的递增区间即为原函数的递减区间.
+kp](k∈Z),而y=sin 2x的递增区间即为原函数的递减区间.
所以,原函数的递减区间为(kp ,kp+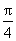 )(k∈Z).
)(k∈Z).
[答案] (kp ,kp+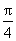 )(k∈Z).
)(k∈Z).
[点评]
本题考查三角函数、对数函数的单调性及复合函数的单调性判断方法.
4.已知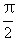 <b
<a <
<b
<a <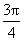 ,cos(a -b )=
,cos(a -b )=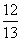 ,sin(a +b
)=-
,sin(a +b
)=-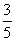 ,则sin 2a 的值为____.
,则sin 2a 的值为____.
[提示]
由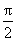 <b
<a <
<b
<a <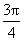 ,得0 <a
-b
<
,得0 <a
-b
<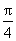 ,p <a
+b <
,p <a
+b <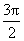 ,根据cos(a -b )=
,根据cos(a -b )=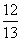 ,有sin(a -b )=
,有sin(a -b )= ;根据sin(a +b
)=-
;根据sin(a +b
)=-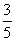 ,有cos(a +b
)=-
,有cos(a +b
)=-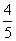 ,
,
所以,sin 2a =sin[(a -b )+(a +b)]
=sin(a -b )cos(a +b )+cos(a -b )sin(a +b )
= ×(-
×(-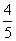 )+(
)+(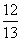 )×(-
)×(-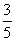 )=-
)=-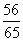 .
.
[答案]-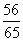 .
.
[点评]
本题考查三角函数的和角公式、同角三角函数关系及运算能力.解题中运用了角的变换,注意到(a +b )+(a -b )=2a ,得sin 2a =sin[(a +b )+(a -b)],用两角和的正弦公式就可以得出sin 2a 的值,变换的思想是数学的基本思想.
3.对于正整数n,f(n)=sin n a +cos n a ,若已知f(1)=a(| sin a +cos a |),
则f(3)=____________.
[提示]
f(1)=sin a +cos a =a,于是,得sin a cos a=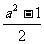 ,
,
从而f(3)=sin3 a
+cos3 a =a(1-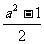 )=
)=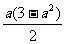 .
.
[答案]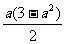 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com