
题目列表(包括答案和解析)
2.求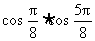 的值等于___________.
的值等于___________.
[提示]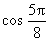 =cos(
=cos(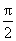 +
+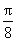 )=-sin
)=-sin 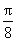 .
.
[答案]- .
.
[点评]本题考查诱导公式,二倍角公式以及特殊角的三角函数值.
1.终边在坐标轴上的角的集合是_________.
[答案]{a | a =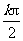 ,k∈Z }
,k∈Z }
[点评]本题考查轴线角的概念.
10.若q 三角形的一个内角,且函数y=x2 cos q -4x sin q +6对于任意实数x均取正值,那么cos q 所在区间是( ).
(A)(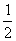 ,1)
(B)(0,
,1)
(B)(0,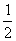 ) (C)(-2,
) (C)(-2,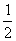 ) (D)(-1,
) (D)(-1,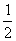 )
)
[提示]
对于任意实数x,函数y均取正值必满足a>b,且判别式 <0<p,有-1<cos
q <1.由不等式组
<0<p,有-1<cos
q <1.由不等式组 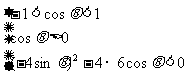
解得 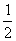 <cos q <1.
<cos q <1.
[答案](A).
[点评]本题结合二次函数的性质考查三角函数的有关知识.
9. 的值等于( ).
的值等于( ).
(A)2 (B)-2 (C)1 (D)-1
[提示]arcsin =
= ,arcos(
,arcos(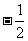 )=
)=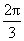 ,arctan(-
,arctan(-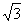 )=-
)=-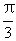 .
.
[答案](C).
[点评]本题考查反正弦.、反余弦、反正切的定义及特殊角的三角函数值.
8.函数y=-3 cos(-2 x+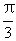 )的图象可由y=-3 cos(-2x)的图象( ).
)的图象可由y=-3 cos(-2x)的图象( ).
(A)向左平行移动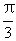 个单位长度得到
个单位长度得到
(B)向右平行移动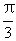 个单位长度得到
个单位长度得到
(C)向左平行移动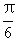 个单位长度得到
个单位长度得到
(D)向右平行移动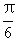 个单位长度得到
个单位长度得到
[提示]y=-3 cos[-2(x-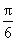 )] =-3 cos(-2x+
)] =-3 cos(-2x+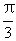 ).
).
[答案](D).
[点评]本题考查三角函数的图象和性质.
7.已知q 是第三象限角,且sin 4 q+cos 4 q = ,那么sin 2q 等于( ).
,那么sin 2q 等于( ).
(A)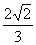 (B)-
(B)-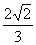
(C) (D)-
(D)-
[提示]
sin4 q+cos4 q =(sin2 q +cos2 q)2-2 sin2 q cos2 q =1-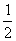 sin2 2q ,得sin2 2q =
sin2 2q ,得sin2 2q =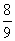 ,再由q
是第 三象限角,判断sin 2q 大于0.
,再由q
是第 三象限角,判断sin 2q 大于0.
[答案](A).
[点评]本题考查同角三角函数公式、二倍角公式及三角恒等变形的能力.
6.在下列函数中,以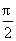 为周期的函数是( ).
为周期的函数是( ).
(A)y=sin 2x+cos 4x
(B)y=sin 2x cos 4x
(C)y=sin 2x+cos 2x
(D)y=sin 2x cos 2x
[提示]可以根据周期函数的定义对四个选项逐个进行验证.
[答案](D).
[点评]本小题考查三角函数的周期性.
由于sin 2(x+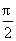 )+cos 4(x+
)+cos 4(x+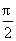 )
)
=sin(2x+p)+cos(4x+2p)
=-sin 2x+cos 4x sin 2x+cos 4x,排除(A);
sin 2x+cos 4x,排除(A);
由于sin 2(x+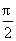 )cos 4(x+
)cos 4(x+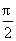 )
)
=-sin 2x cos 4x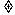 sin 2x cos 4x,排除(B);
sin 2x cos 4x,排除(B);
由于sin 2(x+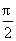 )+cos 2(x+
)+cos 2(x+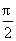 )
)
=-sin 2x-cos 2x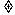 sin 2x+cos 2x,排除(C);
sin 2x+cos 2x,排除(C);
而sin 2(x+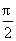 )cos 2(x+
)cos 2(x+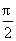 )
)
=sin 2x cos 2x,故选(D).
实际上y =sin 2x cos 2x=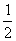 sin 4x,其周期为
sin 4x,其周期为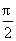 .
.
5.函数y=tan(x+ )的定义域是( ).
)的定义域是( ).
(A){x∈R | x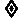 k p+
k p+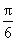 ,k∈Z }
,k∈Z }
(B){ x∈R | x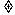 kp-
kp-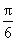 ,k∈Z }
,k∈Z }
(C){ x∈R | x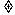 2kp+
2kp+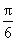 ,k∈Z }
,k∈Z }
(D){ x∈R | x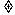 2kp-
2kp-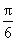 ,k∈Z }
,k∈Z }
[答案](A).
[点评]本题考查正切函数定义域.
4.若b>a>0,且tan a =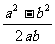 ,sin a =
,sin a =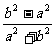 ,则a 的集合是( ).
,则a 的集合是( ).
(A){a | 0<a <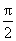 }
}
(B){a |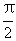 +2k p
+2k p a
a p+2k p,k∈Z}
p+2k p,k∈Z}
(C){a |2k p a
a p+2k p,k∈Z}
p+2k p,k∈Z}
(D){a |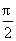 +2k p<a<p+2k p,k∈Z
+2k p<a<p+2k p,k∈Z
[提示]由已知,tan a <0,sin a >0 ,且a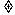 b,即
b,即
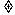 0,故a 是第二象限角.
0,故a 是第二象限角.
[答案](D).
[点评]本题考查由三角函数值的符号确定角所在的象限.
3.Sin 600°的值是( ).
(A)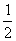 (B)
(B) (C)
(C) (D)
(D)
[提示]sin 600°=sin 240°=-sin 60°=- .
.
[答案](D).
[点评]本题是1998年高考题,主要考查诱导公式及特殊角的三角函数值.利用诱导公式可以把求任意角的三角函数值的问题转化为求某锐角的三角函数值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com