
题目列表(包括答案和解析)
2.(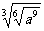 )4(
)4(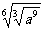 )4等于( )
)4等于( )
(A)a16 (B)a8 (C)a4 (D)a2
1.化简(1+2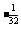 )(1+2
)(1+2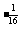 )(1+2
)(1+2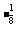 )(1+2-
)(1+2-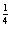 )(1+2
)(1+2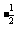 ),结果是( )
),结果是( )
(A)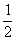 (1-2
(1-2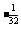 )-1 (B)(1-2
)-1 (B)(1-2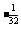 )-1
)-1
(C)1-2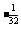 (D)
(D)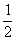 (1-2
(1-2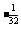 )
)
5.若函数f(x)=a+b cos x+c sin x的图象过(0,1)与(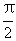 ,1)两点,且x∈[0,
,1)两点,且x∈[0,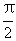 ]时,| f(x)|
]时,| f(x)| 2,求a的取值范围.
2,求a的取值范围.
[提示]
根据函数f(x)的图象经过两个已知点,可得到b、c关于a的表达式,代入f(x)的解析式中,得f(x)=a+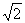 (1-a)sin (x+
(1-a)sin (x+ ),再利用| f(x)|
),再利用| f(x)| 2,可得a的取值范围.
2,可得a的取值范围.
[答案]
∵ 函数f(x)的图象经过点(0,1)及(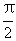 ,1),
,1),
∴ 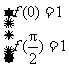 即
即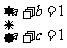 .
.
从而b=c=1-a.
∴ f(x)=a+(1-a)cos x+(1-a)sin x=a+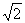 (1-a)sin(x+
(1-a)sin(x+ ).
).
由于x∈[0,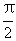 ],得x+
],得x+ ∈[
∈[ ,
,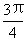 ],
],
∴ sin(x+ )∈[
)∈[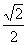 ,1].
,1].
①当a 1时,1-a
1时,1-a 0,f(x)∈[1,a+
0,f(x)∈[1,a+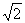 (1-a)],而| f(x)|
(1-a)],而| f(x)| 2,有1
2,有1 f(x)
f(x) 2.
2.
∴ a+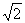 (1-a)
(1-a) 2,
2,
即a∈[-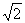 ,1].
,1].
②当a>1时,1-a<0,f (x)∈[a+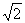 (1-a),1],
(1-a),1],
因f (x) 2,得-2
2,得-2 f (x)
f (x) 1.
1.
∴ -2 a+
a+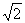 (1-a),
(1-a),
即a∈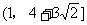 .
.
综上,-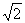
 a
a 4+
4+ 即为所求.
即为所求.
[点评]
本题考查两角和的正弦公式,三角函数的值域以及综合运用函数、不等式等有关知识解决问题的能力.
5.求证 =1+tan 2
a +sin 2
a.
=1+tan 2
a +sin 2
a.
[提示一]通过将右边的式子作“切化弦”的变换.
[提示二]通过化“1”进行变换,可以将sin2 a +cos2 a 化成1,也可以根据需要将1化成sin2 a+cos2 a .
[答案一]右边=1+ +sin2 a
+sin2 a
=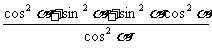
=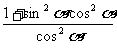
=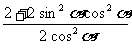
=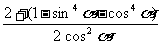
=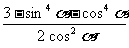 =左边
=左边
[答案二]
左边=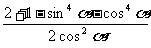
=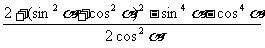
=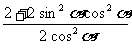
=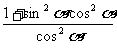
=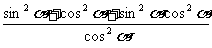
= +1+sin2 a
+1+sin2 a
=1+tan 2 a+sin 2 a
=右边.
[点评]
本题考查三角恒等式的证明.[答案一]和[答案二]均采用了综合法,即从已知条件出发,将左边(或右边)进行恒等交换,逐步化成右边(或左边).本题也可以采用分析法,即从求证的等式出发,递推到已知.
3.已知 =k(
=k( <a
<
<a
<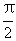
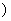 ,试用k表示sin a -cos a 的值.
,试用k表示sin a -cos a 的值.
[提示]
先化简 =2 sin a
cos a
,再利用(sin a -cos a)2=1-2 sin a cos a 即可.
=2 sin a
cos a
,再利用(sin a -cos a)2=1-2 sin a cos a 即可.
[答案]
∵ 
=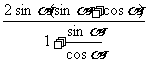
=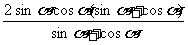
=2 sin a cos a
=sin 2a =k ≤1.
而(sin a-cos a)2=1-sin 2a =1-k,
又 <a
<
<a
<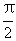 ,于是sin a
-cos a >0,
,于是sin a
-cos a >0,
∴ sin a -cos a =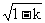 .
.
[点评]
本题考查二倍角公式,同角三角函数关系及运算能力.
2.设a 是第二象限角,sin a =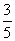 ,求sin (
,求sin (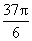 -2a)的值.
-2a)的值.
[提示]因为sin (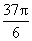 -2a )=sin (6p+
-2a )=sin (6p+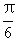 -2a )=sin (
-2a )=sin (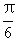 -2a),只要利用已知条件,算出sin 2a,cos 2a 就可以了.
-2a),只要利用已知条件,算出sin 2a,cos 2a 就可以了.
[答案]∵ a 是第二象限角,sin a =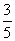 ,
,
∴ cos a =-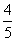 ,
,
∴ sin 2a =2 sin a cos a
=-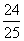 ,
,
cos 2a =1-2 sin2 a = .
.
sin (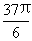 -2a )=sin (
-2a )=sin (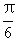 -2a )= sin
-2a )= sin 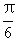 cos 2a
-cos
cos 2a
-cos 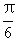 sin 2a =
sin 2a =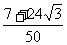 .
.
[点评]本题考查诱导公式,同角三角函数关系式,二倍角公式,两角和与差的正弦余弦,及计算能力.
1.化简(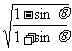 -
-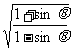 )(
)(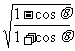 -
-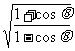 ).
).
[提示]解求题的关键是设法去掉根号,将无理式化为有理式,如
 =
=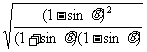 =
=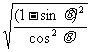 =
=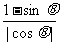 .其它三个根式类似.
.其它三个根式类似.
[答案]
原式=(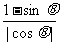 -
-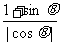 )(
)(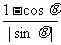 -
-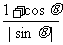 )=
)=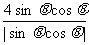 .
.
由题设,sin q cos q
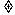 0,
0,
当sin q 与cos q 同号,即kp<q<kp+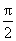 (k∈Z)时,原式=4;
(k∈Z)时,原式=4;
当sin q 与cos q 异号,即kp<q<kp+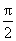 (k∈Z)时,原式=-4.
(k∈Z)时,原式=-4.
[点评]本题考查三角函数值的符号、同角三角函数公式以及三角函数的恒等变形的能力.本题也可将结果进一步化为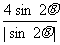 直接讨论sin 2q 符号.
直接讨论sin 2q 符号.
5.函数y=2 sin x cos x-2 sin2 x+1的最小正周期T =__________.
[提示]y=sin 2x+cos 2 x =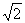 sin(2 x+
sin(2 x+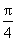 ).
).
[答案]p.
[点评]本题考查二倍角正弦余弦,两角和的三角函数及三角函数y=Asin(w x+j)的周期性.
4.若sin(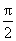 +a)=
+a)=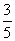 ,则cos 2a =__________.
,则cos 2a =__________.
[提示]依题意,cos a =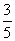 ,则cos 2 a=2 cos2 a
-1=-
,则cos 2 a=2 cos2 a
-1=- .
.
[答案]- .
.
[点评]本题考查诱导公式与二倍角余弦公式.
3.tan 20°+tan 40°+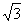 tan 20°tan 40°的值是___________.
tan 20°tan 40°的值是___________.
[提示]利用公式tan(a+b ) = 的变形
的变形
tan a+tan b=tan(a+b )(1-tan a tan b),得
tan 20°+tan 40°+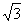 (tan 20°tan 40°)
(tan 20°tan 40°)
=tan(20°+40°)(1-tan 20°tan 40°)+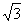 tan 20°tan 40°=
tan 20°tan 40°=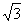 .
.
[答案]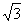 .
.
[点评]本题通过两角和的正切公式的逆向使用考查三角恒等式的变形及计算推理能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com