
题目列表(包括答案和解析)
6.Y=4x-3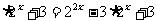 ,依题意有
,依题意有
 即
即 ,∴ 2
,∴ 2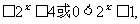
由函数y=2x的单调性可得x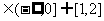 。
。
5.令y=(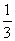 )U,U=x2+2x+5,则y是关于U的减函数,而U是(-
)U,U=x2+2x+5,则y是关于U的减函数,而U是(- ,-1)上的减函数,[-1,+
,-1)上的减函数,[-1,+ ]上的增函数,∴ y=(
]上的增函数,∴ y=(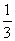 )
)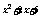 在(-
在(- ,-1)上是增函数,而在[-1,+
,-1)上是增函数,而在[-1,+ ]上是减函数,又∵U=x2+2x+5=(x+1)2+4
]上是减函数,又∵U=x2+2x+5=(x+1)2+4 4, ∴y=(
4, ∴y=(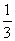 )
)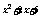 的值域为(0,(
的值域为(0,(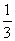 )4)]。
)4)]。
4.要使f(x)为奇函数,∵ x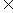 R,∴需f(x)+f(-x)=0, ∴f(x)=a-
R,∴需f(x)+f(-x)=0, ∴f(x)=a- =a-
=a-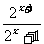 ,由a-
,由a- =0,得2a-
=0,得2a-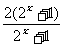 =0,得2a-
=0,得2a-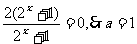 。
。
3.f(x)=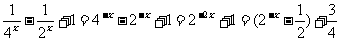 , ∵x
, ∵x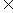 [-3,2], ∴
[-3,2], ∴ .则当2-x=
.则当2-x=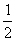 ,即x=1时,f(x)有最小值
,即x=1时,f(x)有最小值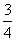 ;当2-x=8,即x=-3时,f(x)有最大值57。
;当2-x=8,即x=-3时,f(x)有最大值57。
2.g[g(x)]=4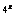 =4
=4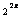 =2
=2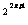 ,f[g(x)]=4
,f[g(x)]=4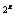 =2
=2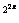 ,∵g[g(x)]>g[f(x)]>f[g(x)],
∴2
,∵g[g(x)]>g[f(x)]>f[g(x)],
∴2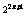 >2
>2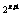 >2
>2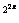 ,∴22x+1>2x+1>22x,
∴2x+1>x+1>2x,解得0<x<1
,∴22x+1>2x+1>22x,
∴2x+1>x+1>2x,解得0<x<1
1.∵0<a<2,∴
y=ax在(- ,+
,+ )上为减函数,∵ a
)上为减函数,∵ a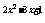 >a
>a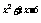 , ∴2x2-3x+1<x2+2x-5,解得2<x<3,
, ∴2x2-3x+1<x2+2x-5,解得2<x<3,
11.∵ g(x)是一次函数,∴可设g(x)=kx+b(k 0), ∵F(x)=f[g(x)]=2kx+b。由已知有F(2)=
0), ∵F(x)=f[g(x)]=2kx+b。由已知有F(2)=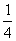 ,F(
,F(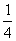 )=2,∴
)=2,∴  ,∴ k=-
,∴ k=-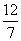 ,b=
,b=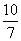 ,∴f(x)=2-
,∴f(x)=2-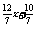
10.2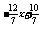
9.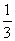 或3。
或3。
Y=m2x+2mx-1=(mx+1)2-2,
∵它在区间[-1,1]上的最大值是14,∴(m-1+1)2-2=14或(m+1)2-2=14,解得m=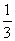 或3。
或3。
8.0 f(125)=f(53)=f(52×2-1)=2-2=0。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com