
题目列表(包括答案和解析)
8.在等比数列{an}中,a3和a5是二次方程x2+kx+5=0的两根,则a2a4a6的值为
(A) (B)
(B) (C)
(C) (D)25
(D)25
7.已知g(x2+1)=x4+x2-6,那么g(x2+1)的最小值为
(A)g(0)
(B)g(1)- (C)g(1)+
(C)g(1)+ (D)g(1)
(D)g(1)
6.已知等差数列{an}的首项为a1=1,公差d≠0,如果a1,a2,a5成等比数列,那么d等于
(A)3 (B)-2 (C)2 (D)2或-2
5.当0<x<1时,函数 与其反函数y=f-1(x)对应的函数值的大小关系是
与其反函数y=f-1(x)对应的函数值的大小关系是
(A)f(x)>f-1(x) (B)f(x)=f-1(x) (C)f(x)<f-1(x) (D)不能确定
4.在数列{an}中,已知a1=1,an+1=2an+1,则{an}的通项为
(A)2n-1 (B)2n (C)2n+1 (D)2n-1
3.将函数y=2-x的图象向左平移1个单位,再向上平移3个单位,所得图象的解析式为
(A)y=2-x+1+3 (B)y=2-x+1-3 (C) (D)y=2x+1+3
(D)y=2x+1+3
2.已知f(x)=2x+3,g(x+2)=f(x),则g(x)等于
(A)2x+1 (B)2x-1 (C)2x-3 (D)2x+7
1.已知U为全集,集合M、N是U的子集,若M∩N=N,则
(A) (B)
(B)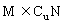 (C)
(C) (D)
(D)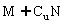
20. (本小题满分12分)
(1) 画出函数g (x ) = x2 – 2|x| 的图象;
(2) 证明函数f ( x ) = x +  在(0,1]上单调递减.
在(0,1]上单调递减.
21 (本小题满分14分)
某次国际网球邀请赛共有128位选手参加,比赛采用单淘汰制,即每轮淘汰一半的选手,剩下一半的选手进入下一轮. 在第1轮被淘汰的每位选手可获得出场费1万元,在第2轮被淘汰的选手可获得2万元,在第k轮被淘汰的选手可获得2 k – 1 万元,而冠军则可获得128万元.
(1)求本次网球邀请赛共需出场费多少万元?
(2)设网球场有3000个坐位,第一轮比赛门票价格为a元( a为整数),第二轮比赛门票价格为a + 50元,第k轮比赛门票价格为a + 50(k – 1 )元. 假设每场比赛均满座,且每张门票可观看一轮的所有比赛,则要使本次邀请赛不亏本,第一轮门票价格a应该如何确定?
19. (本小题满分8分)
设i , j 是平面直角坐标系内x轴,y轴正方向上的两个单位向量,且 = 4i + 2j ,
= 4i + 2j , = 3i + 4 j . 试证:△ABC是直角三角形.
= 3i + 4 j . 试证:△ABC是直角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com