19．设这个摊主每天从报社买进x份报纸，每月所获的利润为y元，则由题意可知250x400,且y=0.3×x×20+0.3×250×10+0.05×(x-250) ×10-0.2×x×30=0.5x+625。

∵ 函数f(x)在[250，400]上单调递增，∴当x=400时，y最大=825，即摊主每天从报社买进400份报纸可获得最大利润，最大利润为825元。

18．(1)∵，∴ -1<x<1,即f(x)的定义域为(-1，1)。

(2)∵x(-1,1)且f(-x)=log_a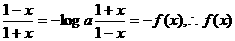为奇函数。

17．∵ a、b、c成等差数列，∴ 2b=a+c……①。又∵a、b、c成等比数列，∴ c²=ab……②,①②联立解得a=-2c或a=-2c或a=c(舍去)，b=-,a∶b∶c=(-2c)∶(- )∶c=-4∶-1∶2。

13．　　　 14.　64　　 15.　(0,1) 16.　5

21．数列{a_n}的通项公式a_n=,f(n)=(1-a₁)(1-a₂)(1-a₃)……(1-a_n)。

(1)求f(1),f(2),f(3),f(4),并猜想f(n)的表达式；

(2)用数字归纳法证明你的结论。(本题10分)

20．设有两个集合A={x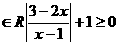},B={x},若A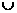B=B，求a的取值范围。(本题10分)

19．北京市的一家报刊摊点，从报社买进《北京日报》的价格是每份0.20元，卖出的价格是每份0.30元，卖不掉的报纸可以以每份0.05元的价格退回报社。在一个月(以30天计算)里，有20天每天可卖出400份，其余10天每天只能卖出250份，但每天从报社买进的份数必须相同，这个推主每天从报社买进多少份，才能使每月所获的利润最大？并计算他一个月最多可赚得多少元？(本题10分)

18．已知函数f(x)=loga.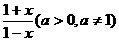

(1)求f(x)的定义域；

(2)判断并证明f(x)的奇偶性。(本题10分)

17．三个不同的实数a、b、c成等差数列，且a、c、b成等比数列，求a∶b∶c.(本题8分)

16．定义运算法则如下：

a则M+N=