
题目列表(包括答案和解析)
6、已知函数y=3(x-1)2的图象为C1,y=3(x+1)2的图象为C2,那C2的图象是由C1的图象( )得到的.
A.向左平移1个单位 B.向右平移1个单位
C.向左平移2个单位 D.向右平移2个单位
5、函数y=sin2x的图象按向量a平移后,所得函数的解析式是y=cos2x+1,则a等于( )
A.( ,1)
B.(-
,1)
B.(- ,1) C.(-
,1) C.(-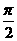 ,1) D.(
,1) D.(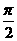 ,1)
,1)
4、将函数y=f(x)图象上的点P(1,0)平移变为P'(2,0),平移后得到新图象的函数解 析式为 ( )
A.y'=f(x'-1) B.y'= f(x')-1 C.y'=f(x'+1) D.y'=f(x')+1
3、函数f(x)=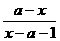 的反函数f -1(x)的图象的对称中心是(-1,3),则实数a等于 ( )
的反函数f -1(x)的图象的对称中心是(-1,3),则实数a等于 ( )
A.2 B.3 C.-2 D.-4
2、点P(2,-1)平移后变成了P'(-2,1),则坐标原点平移后对应点的坐标是 ( )
A.(4,2) B.(4,-2) C.(-4,2) D.(-4,-2)
1、将点(2,-5)按向量a=(-3,4)平移后得对应点的坐标为 ( )
A.(-1,-1) B.(5,-9) C.(-1,-9) D.(5,-1)
22. 分析:要求AD的长,关键在于求出D点坐标,而由平面几何中三角形内角平分线性质定理有|AC|:|AB|=|CD|:|DB|可求出D点分CB所成的比,再由定比分点公式即可求出D点坐标.
解:∵ =
= ,
,  =
=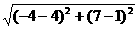
又λ=  =
= =
=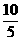 = 2.
= 2.  即D(
即D( ,
, )
)
因此
 =
= 
注:在本例中还可以求出∠A的外角平分线与CB延长线的交点坐标等.
21. 解:①设a= n-1,b= n, c= n+1,n∈N,且n>1. ∵C为钝角,
∴ cosC = 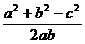 =
= 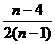 <0. ∵1<n<4 , n∈N, ∴ n= 2 或3.
<0. ∵1<n<4 , n∈N, ∴ n= 2 或3.
当n=2时,
a=1,b=2,c=3,不能构成三角形. 当n= 3时,a= 2,b= 3,c=
4. cosC=- ,
,
由查表或计算器得最大角C=109°29'. ②设夹角C的两边为x,y,则x+y=4,
则平行四边形的面积S= xysinC=x(4-x)× , ∴ 当x = 2时, S max =
, ∴ 当x = 2时, S max =  .
.
注:余弦定理可以判断三角形中的角是锐角,钝角或直角. cosA>0,则∠A为锐角,cosA<0,则∠A为钝角,cosA=0,则∠A为直角.
20. 以21海里/小时, 沿东偏北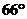 47’ 航行.
47’ 航行.
②k
 = k(1,0)-(2,1)=(k-2,-1).
设k
= k(1,0)-(2,1)=(k-2,-1).
设k
 =λ(
=λ( ),即(k-2,-1)=
λ(7,3),
),即(k-2,-1)=
λ(7,3),
∴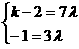
 . 故k=
. 故k=  时, 它们反向平行.
时, 它们反向平行.
18. =2×1×
=2×1× =1. ∵
=1. ∵ 与
与 垂直,
垂直,
∴( )
) =
= 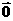 , ∴2
, ∴2
 k = - 5.
k = - 5.
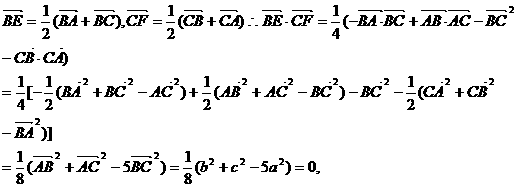 ∴
∴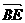 ⊥
⊥ , 即 BE⊥CF .
, 即 BE⊥CF .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com