
题目列表(包括答案和解析)
(17)(本小题满分12分)
求不等式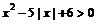 。
。
(18)(本小题满分12分)
设集合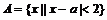 ,
, ,若
,若 ,求实数
,求实数 的取值范围。
的取值范围。
(19)(文科)(本小题满分12分)
已知 ,
, ,求
,求 的值。
的值。
(理科)(本小题满分12分)
求函数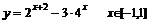 的值域。
的值域。
(20)(文科)(本小题满分12分)
求函数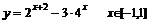 的值域。
的值域。
(理科)(本小题满分12分)
若奇函数 在定义域
在定义域 上是减函数,求:
上是减函数,求:
① 函数 及
及 的定义域;
的定义域;
② 满足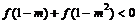 的实数
的实数 的取值范围。
的取值范围。
(21)(文科)(本小题满分12分)
若奇函数 在定义域
在定义域 上是减函数,求:
上是减函数,求:
① 函数 及
及 的定义域;
的定义域;
② 满足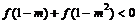 的实数
的实数 的取值范围。
的取值范围。
(理科)(本小题满分12分)
已知 ,若
,若 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为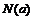 ,令
,令 。
。
① 求 的解析式;
的解析式;
② 判断 的单调性,并求出
的单调性,并求出 的最小值。
的最小值。
(22)(文科)(本小题满分14分)
已知 ,若
,若 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为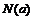 ,令
,令 。
。
① 求 的解析式;
的解析式;
② 判断 的单调性,并求出
的单调性,并求出 的最小值。
的最小值。
(理科)(本小题满分14分)
设f (x)
= 2(log2x)2 + 2alog2 + b,已知x =
+ b,已知x = 时,f (x) 有最小值 –8.
时,f (x) 有最小值 –8.
① 求a与b的值; ② 在 ① 的条件下,求f (x) > 0的解集A;
③ 集合B ={x| | x –t |≤ ,x
,x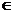 R},且A
R},且A B =
B = ,求实数t 的取值范围.
,求实数t 的取值范围.
(附加题,满分10分,不计入总分)
已知二次函数f (x) = ax2 +bx + c (a、b、c均为实数),且同时满足下列条件:
① f (–1) = 0;② 对任意实数x,都有f (x) –x≥0;③ 当x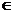 (0,2)时,有f (x)≤(
(0,2)时,有f (x)≤(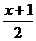 )
)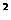 .
.
(1) 求f (1); (2) 求a、b、c 的值;
(3) 当x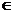 [–1,1] 时,函数g (x) = f (x) –mx (m是实数)是单调函数,求m 的取值范围.
[–1,1] 时,函数g (x) = f (x) –mx (m是实数)是单调函数,求m 的取值范围.
(13)函数 的反函数为
.
的反函数为
.
(14)函数f (x) 对任何x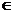 R+ 恒有f (x1·x2) = f (x1) + f (x2),已知f (8) = 3,则f (
R+ 恒有f (x1·x2) = f (x1) + f (x2),已知f (8) = 3,则f ( ) =_____.
) =_____.
(15)已知函数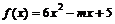 在区间
在区间 上是增函数,则
上是增函数,则 的取值范围是
.
的取值范围是
.
(16)如果函数 的定义域为
的定义域为 ,则实数
,则实数 的范围是
.
的范围是
.
(1)已知集合 ,那么集合
,那么集合 为
为
(A) x = 3,y = –1 (B) {3,–1} (C) (3,–1) (D) {(3,–1)}
(2)不等式 的解集为
的解集为
(A) (B)
(B)
(C)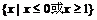 (D)
(D)
(3)若 、
、 是两个简单命题,且“
是两个简单命题,且“ 或
或 ”的否定是真命题,则必有
”的否定是真命题,则必有
(A)  真
真 真
(B)
真
(B)  假
假 假
(C)
假
(C)  真
真 假
(D)
假
(D)  假
假 真
真
(4)“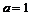 ”是“函数
”是“函数 的最小正周期为
的最小正周期为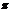 ”的
”的
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既非充分又非必要条件
(5)下列各项中能表示同一函数的是
(A) 与
与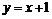 (B)
(B) 与
与
(C)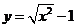 与
与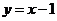 (D)
(D) 与
与
(6)已知 ,则
,则
(A) (B)
(B) (C)
(C)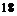 (D)
(D) 
(7)若 区间
区间 上
上
(A)单调递增 (B)单调递减 (C)先增后减 (D)先减后增
(8)设 是
是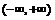 上的奇函数,
上的奇函数, ,当
,当 时
时 ,则
,则 等于
等于
(A)0.5 (B)-0.5 (C)1.5 (D)-1.5
(9)已知二次函数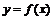 满足
满足 ,且有两个实根
,且有两个实根 ,
,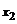 ,则
,则 =
=
(A)0 (B)3 (C)6 (D)不确定
(10)函数 的增区间是
的增区间是
(A) (B)
(B) (C)
(C) (D)
(D)
(11)若函数 的值域是
的值域是 ,则实数
,则实数 的取值范围是
的取值范围是
(A) (B)
(B) (C)
(C)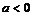 或
或 (D)
(D) 或
或
(12)已知函数 ,则它的反函数
,则它的反函数 的图象是
的图象是
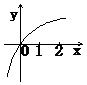

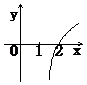

(A) (B) (C) (D)
第Ⅱ卷(非选择题 共90分)
22、已知函数 是奇函数,且
是奇函数,且 .
.
(1)求函数f(x)的解析式;
(2)指出函数f(x)的单调区间,并加以证明.
21、福兴公司从2002年起,每人的年工资已由三个项目组成并按下表规定实施
|
项 目 |
计 算 办 法 |
|
基本工资 |
2002年1万元,考虑物价因素,以后每年递增10% |
|
住房补贴 |
按在公司工作年限计算:在公司工作第一年补3600元,以后每年比上年多500元(工作年限计算办法,如某职工1999年进公司,到2002年按4年计算) |
|
医疗补贴 |
每年2400元,固定不变 |
现有一位职工李某2003年到该公司工作,假设李某以后一直在该公司工作,那么2012年,李某的年工资是多少元?(提示:计算时可取: ,
, ,
, )
)
解:
20、用长为 m的铁丝弯成下部为矩形,上部为半圆型的框架,若矩形的底边AB的长为 2x,求此框架围成的面积y与x的函数解析式,并写出它的定义域.
解:
19、公差d不为零的等差数列{an}的第二、第三、第七项恰好构成等比数列,求这个等比数列的公比q .
解:
18、解关于x的不等式:
解:
17、计算下列各式:
(1) -4×
-4×
(2)化简:
解:
16、有下列四个命题:
①空集是任何集合的真子集;
②命题“面积相等的三角形全等”的否命题;
③若命题p的逆命题是q,命题p的否命题是r,则q是r的逆否命题;
④2与8的等比中项是4 .
其中正确命题的序号是_______________. (把你认为正确命题的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com