7. 某人从2003年起，每年1月14日到银行新存入a元(一年定期). 若年利率为r保持不变，且每年到期存款均自动转为新的一年定期，到2008年1月14日将所有存款及利息全部取回(不考虑利息税)，他可取回的钱数为

(A) a (1 + r)⁵元  (B) 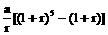元

(C) a (1 + r)⁶元 (D)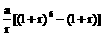元

6. 若指数函数满足f (- 2) = 4, 则f^-1 (x)的解析式是

(A) f^-1 (x) = log₂x 　　　 (B) f^-1 (x) = log₄x

(C) f^-1 (x) =－log₂x 　 　 (D) f^-1 (x) =－log₄x

5. 已知等差数列{a_n}满足a₁ + a₂ + … + a₉₁ = 0，则有

　 (A) a₃ + a₈₉ = 0　 (B) a₂ + a₉₀ < 0　 (C) a₁ + a₉₁ > 0 　 (D) a₄₆ = 46

4. 设1< a < b < c则下列不等式中正确的是

　(A) c^a < b^a　 　　 (B)　 a^c > a^b　 　(C) log_cb < log_ca　　 (D) log_ca > log_ba

3. 函数y=－lg(1－x )的定义域是

　(A) [-3, 　　　　(B) (2, 3)　　　 (C) (3, +¥)　　 　 (D) (1, 2)

2. 命题“若a = 0，则ab = 0”的逆否命题是　　　　　　 .

(A)若ab = 0，则a = 0　 (B)若a≠0, 则ab≠0

(C)若ab = 0,　 则a≠0　 (D)若ab≠0，则a≠0

1. 设集合P = {(x, y)| y = x²}, 集合Q = {(x, y)| y = x}则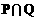等于

(A)　 {(0, 0)}　　 　　(B) {(1,1)}

(C) {(0,0),(1,1)}　 　　 (D) {(0,1)}

19．B(普通校学生做，重点校学生不做。本小题满分8分)

　已知a、b为常数，且a≠0，函数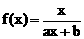，且f(3)=1，又方程f(x)=x有唯一解。

　(I)求f(x)的解析式及方程f(x)=x的解；

　(II)当，数列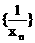是何数列？请说明理由。

19．A(重点校学生做，普通校学生选做，本小题满8分)

　已知二次函数满足f(1)=0。

　(I)若a>b>c，证明f(x)的图象与x轴有两个交点，且这两个交点间的距离d满足：；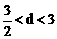

　(II)设f(x)在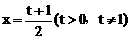处取得最小值，且对任意实数x，等式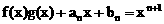(其中n∈N，)都成立，若数列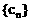的前n项和为，求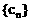的通项公式。

18．(本小题满分7分)

　已知等比数列的各项都是正数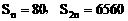，，且在前n项中，最大项的值为54，求n的值。