
题目列表(包括答案和解析)
17. 求不等式组 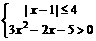 的解集.
的解集.
16. 对于任意定义在R上的函数f (x),若实数x0满足f (x0) = x0,则称x0是函数f (x)的一个不动点,若函数f (x)= ax2 + (2a – 3)x + 1恰有一个不动点,则实数a的取值集合是_________________ .
15. 已知-9, a1, a2, -1四个实数成等差数列,-9, b1, b2, b3, -1五个实数成等比数列,则b2(a2-a1)等于______________ .
14. 设数列{a n}的前n项和Sn =-n 2 + 1 , 那么此数列的通项公式a n = _________________.
13. 2log525 + 3log264-lg(log3310) = _______________.
12. 各项都是正数的等比数列{an}中,a2, 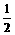 a3,
a1成等差数列,则
a3,
a1成等差数列,则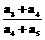 的值是
的值是
(A) 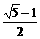 (B)
(B) 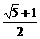 (C)
(C) 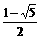 (D)
(D) 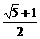 或
或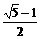
11. 在各项都不等于零的等差数列{an}中,若m > 1,且am-1 + am+1-am2 = 0, S2m-1 = 38,则m等于
(A) 38 (B) 20 (C) 10 (D) 9
10. 若函数f (x)的图象与函数g (x)=(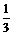 )x的图象关于直线y = x对称,则f (2x-x2)的单调递减区间是
)x的图象关于直线y = x对称,则f (2x-x2)的单调递减区间是
(A)[2, +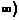 (B) (0,
(B) (0, 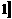 (C) [1,
(C) [1, 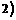 (D)(-∞, 0)
(D)(-∞, 0)
9. 方程x2
+ x =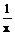
(A)无实根 (B) 有异号两根 (C) 仅有一负根 (D) 仅有一正根
8. 设f (x), g (x)都是定义在R上的单调函数,有如下四个命题:
①若f (x)单调递增,g (x)单调递增,则f (x)·g (x)单调递增;
②若f (x)单调递增,g (x)单调递减,则f (x)-g (x)单调递增;
③若f (x)单调递减,g (x)单调递增,则f (x)-g (x)单调递减;
④若f (x)单调递减,g (x)单调递增且g (x)≠0,则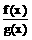 单调递减. 其中正确命题的序号是
单调递减. 其中正确命题的序号是
(A) ①②③ (B) ②③④ (C) ②③ (D) ①②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com