
题目列表(包括答案和解析)
6.某露天剧场有28排座位,每相邻两排座位数相同,第一排有24个座位,以后每隔一排增加两个座位,则全剧场共有座位( ).
(A)1036个 (B)1428个 (C)854个 (D)518个
[提示]由题意知第一、二排,第三、四排,…,第二十七,二十八排的座位数组成等差数列{an},其中a1=24×2,d=2×2,n=14,则S14 可求.
[答案](A).
5.设{an}是由正数组成的等比数列,公比q=2,且a1·a2·a3·…a30=230,那么a3·a6·a9·…·a30 等于( ).
(A)210 (B)215 (C)216 (D)220
[提示]设a1·a4·a7·…·a28=x,则a2·a5·a8·…a29=x·210,a3·a6·a9·…·a30=x·220.于是230=x·(x·210)·(x·220)=x3·230,∴ x=1.
[答案](D).
4.等差数列{an}的前m 项和为30,前2 m 项和为100,则它的前3 m 项和为( ).
(A)130 (B)170 (C)210 (D)260
[提示]设前m 项和V1,m+1到2 m 项和V2,2 m+1到3 m 项和V3,则V1,V2,V3 也成等差数列.于是V1=30,V2=70,d=40.∴ V3=110.
[答案](C).
3.已知数列1,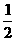 ,
,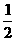 ,
,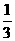 ,
,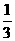 ,
,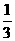 ,
,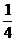 ,
,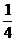 ,
,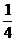 ,
,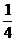 ,…,则此数列前100项的和等于( ).
,…,则此数列前100项的和等于( ).
(A)13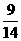 (B)13
(B)13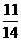 (C)14
(C)14 (D)14
(D)14
[提示]将数列分成n
组:第一组:1,第二组: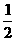 ,
,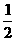 ,第三组
,第三组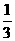 ,
,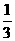 ,
,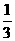 ,…,由于第n 组中有n
个数,且求前100项和,故令1+2+3+…+n=100.即
,…,由于第n 组中有n
个数,且求前100项和,故令1+2+3+…+n=100.即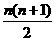 =100,估值可知n=13.即前13组中共有91个数,再加上第14组中前9个数,恰为100项,
=100,估值可知n=13.即前13组中共有91个数,再加上第14组中前9个数,恰为100项,
[答案](A).
2.若数列{an}前8项的值各异,且an+8=an 对任意的n 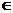 N都成立,则下列数列中可取遍{an}前8项值的数列为( ).
N都成立,则下列数列中可取遍{an}前8项值的数列为( ).
(A){a2 k+1} (B){a3 k+1} (C){a4 k+1} (D){a5 k+1}
[提示]由已知,只需研究2 k+1、3 k+1、4 k+1、5 k+1被8除的余数是1到8的数.故3 k+1型的数符合此条件.
[答案](B).
1.数列{an}中,a1=13,a2=56,an+2=an+1-an,则a1999 等于( ).
(A)-56 (B)-43 (C)13 (D)-13
[提示]求出数列前若干项,分析其中的规律,其数值是周期性变化.
[答案](C).
22.已知数列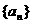 的通项公式为
的通项公式为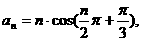 记
记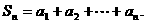
求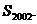
21.设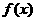 满足
满足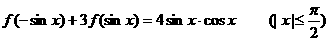 ,
,
求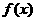 的表达式.
的表达式.
20.已知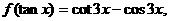
(1)求 的表达式;
的表达式;
(2)求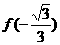 的值.
的值.
19.已知 、
、 是关于
是关于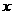 的方程
的方程 的两实根,且
的两实根,且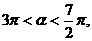
求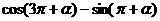 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com