
题目列表(包括答案和解析)
⒈下列各式中错误的是
A、{2,4,6,8}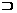 {2,4}
B、d
{2,4}
B、d {a,b,c} C、
{a,b,c} C、
 Q D、
Q D、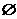
 {0}
{0}
⒉已知全集U,M,N是U的非空子集,并且CUM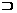 N,则必有
N,则必有
A、M CUN
B、M
CUN
B、M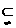 CUN C、CUM=CUN
D、 M=N
CUN C、CUM=CUN
D、 M=N
⒊已知命题P:3≥3;命题q: 3>4,则下列选项正确的是
A、p或q为真,p且q为真,非p为假
B、p或q为真,p且q为假,非p为真
C、p或q为真,p且q为假,非p为假
D、p或q为假,p且q为假,非p为假
⒋ x>1是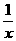 <1的
<1的
A、必要但不充分条件 B、充分但不必要条件
C、充要条件 D、非充分非必要条件
⒌下列各组函数中,表示同一个函数的是
A、f(x)=1, g(x)=x0
B、 f(x)=x+2, g(x)=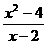
C、f(x)=|x|, g(x)= 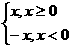 D、f(x)=x, g(x)=
D、f(x)=x, g(x)=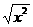
⒍已知集合M={(x ,y
)|x + y =2 },N={(x , y)| x-y=4},那么M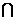 N为
N为
A、x=3,y=-1 B、(3 , -1) C、{ 3, -1 } D、{( 3 , - 1 )}
⒎若不等式ax2+bx+2>0的解集为(-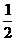 ,
,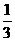 ),那么a+b的值为
),那么a+b的值为
A、10 B、-10 C、14 D、-14
⒏已知U为全集,A、B为U的子集,下列命题中不正确的是:
① 若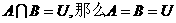 ②
②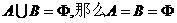
③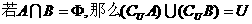 ④
④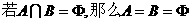
⑤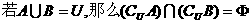 ⑥
⑥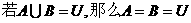
A ④⑤ B ②⑤ C ④⑥ D ①④
⒐满足不等式2(|2x-1|+3)>3(4-|2x-1| )的x的集合是
A、(-
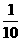 ,
, 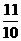 )
B、(
)
B、( 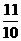 , + ∞)
, + ∞)
C、(-∞ , -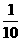 ) D、(-∞, -
) D、(-∞, -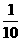 )
) (
( 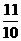 ,+∞ )
,+∞ )
⒑函数f(x)的定义域是[-1 ,1],则函数g(x)=f(1-x)+f(1-x2)的定义域为
A、(0 ,2) B、[0 ,  ]
]
C、[- ,
, ] D、 [0 , 1]
] D、 [0 , 1]
⒒已知二次函数f(x) =x2 -x+a (a为常数),若f(-m )< 0,则f(m+1)的值为:
A、正数 B、负数 C、非负数 D、正数或负数
⒓如果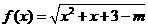 的定义域为R,
的定义域为R,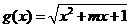 的值域为 [0,+∞)则m的取值范围是:
的值域为 [0,+∞)则m的取值范围是:
A、m≥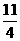 B、m≤-2或m≥2
B、m≤-2或m≥2
C、m≤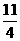 D、m≤-2或2≤m ≤
D、m≤-2或2≤m ≤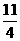
15.已知数列{an}的通项公式,an=(n+1)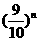 ,问n 取何值时,an 取最大值.
,问n 取何值时,an 取最大值.
[提示]方法一:不妨设an 最大,则 ,由此解得n=8或9.
,由此解得n=8或9.
方法二:先分析{an}的单调性,an+1-an=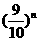 ·
·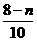 ,再对n 分三类讨论,即n
<8时;n=8时,an 增函数,n>8时,an 是减函数,进而得出结论.
,再对n 分三类讨论,即n
<8时;n=8时,an 增函数,n>8时,an 是减函数,进而得出结论.
14.已知等差数列{an}的首项为a1=21,公差d=-4.
(1)若|a1|+|a2|+…+|ak|=102,求k 的值;
(2)设{an}的前n 项和为Sn,试问数列{Sn}是否存在相同的两项,若存在,求出这样的两项,若不存在,说明理由.
[提示](1)易知an=25-4 n,令an≥0,则n≤6,即前6项为正数,从第7项开始为负数.
∴ |a1|+|a2|+…+|ak|=(a1+a2+…+a6)-(a7+a8+…+ak)
=2 k2-23 k+132=102.
解得
k=10或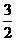 (舍去)
(舍去)
(2)假设存在m,n(m,n 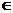 N),使Sm=Sn(m ≠n).则可以推出2 m+2 n=23,对于m,n
N),使Sm=Sn(m ≠n).则可以推出2 m+2 n=23,对于m,n 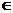 N,此式不可被成立,故{Sn}不存在相同的两项.
N,此式不可被成立,故{Sn}不存在相同的两项.
[答案](1)k=10;(2)不存在相同的两项.
13.已知二次函数f(x)=x2-2(10-3 n)x+9 n2-61 n+100(n 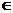 N)
N)
(1)设函数y=f(x)图象的顶点的横坐标组成数列{an},求数列{an}的通项公式an.
(2)设函数y=f(x)图象的顶点到y 轴的距离构成数列{bn},求数列{bn}的前n 项和.
[提示](1)an=10-3 n .
(2)bn=|an|=|10-3 n|=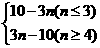
当n≤3时,Sn=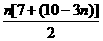 =
=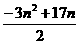 ;
;
当n≥4时,Sn=S3+b4+…+bn=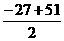 +
+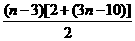
=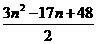 .
.
12.已知数列{an}中,Sn 是它的前n
项和,且Sn+1=4 an+2,(n 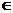 N),a1=1.
N),a1=1.
(1)设bn=an+1-2 an,(n 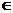 N),求证:数列{bn}是等比数列;
N),求证:数列{bn}是等比数列;
(2)设cn=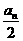 ,(n
,(n 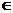 N),求证:数列{cn}是等差数列.
N),求证:数列{cn}是等差数列.
[提示](1)由题意,得Sn+2-Sn+1=4 an+1-4 an,
即 an+2=4 an+1-4 an,变形得an+2-2 an+1=2(an+1-2 an),
即 bn+1=2 bn,再由已知,bn=3·2n-1
(2)由cn= ,得cn+1-cn=
,得cn+1-cn=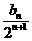 ,又 bn=3·2n-1,故cn+1-cn=
,又 bn=3·2n-1,故cn+1-cn=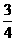 .
.
11.设n 个数成等比数列,P 是这n 个数的乘积,S 是这n 个数的和,S′是这n 个数的倒数和,那么P 等于______________.
[提示]P=a1n·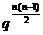 ,S=
,S= .
.
S′=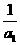 ·
·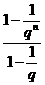 =
=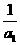 ·
·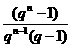 .
.
∴ 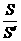 =a12qn-1,
=a12qn-1,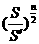 =
=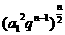 =a1n·
=a1n·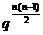 =P .
=P .
[答案]P=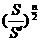 .
.
10.已知数列1,(1+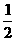 ),(1+
),(1+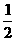 +
+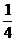 ),(1+
),(1+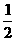 +
+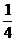 +
+ ),…,(1+
),…,(1+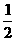 +
+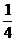 +…+
+…+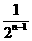 ).则此数列的前n 项和Sn=______________.
).则此数列的前n 项和Sn=______________.
[提示]∵ an=1+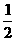 +
+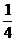 +…+
+…+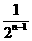 =2-
=2-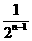
∴ Sn=2 n-(1+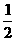 +
+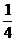 +…+
+…+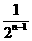 ).
).
[答案]Sn=2 n-2+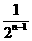 .
.
9.在数列{an}中,a1=1,Sn=n2an ,则an=______________.
[提示]当n≥2时,an=Sn-Sn-1=n2an-(n-1)2 an-1
∴ 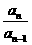 =
=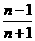 ,从而
,从而 =
=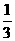 ,
, =
= ,
,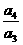 =
=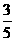 ,…,
,…,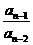 =
=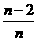 ,
,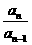 =
=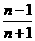 ,将以上n-1个等式相乘,得
,将以上n-1个等式相乘,得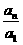 =
=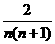 .
.
[答案]an=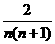 .
.
8.两个等差数列,它们的前n 项和之比为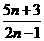 ,则这两个数列的第九项的比是_________.
,则这两个数列的第九项的比是_________.
[提示]设两数列为{an}、{bn},相应的前n 项和为Sn、Tn 则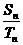 =
=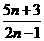 ,
,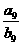 =
=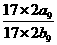 =
=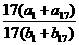 =
=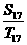 =
=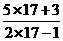 =
=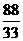 =
=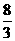 .
.
[答案]8︰3.
7.已知a>b>0,A 是a、b 的等差中项.G 是a、b 的等比中项,且G>0,若A=
2 G .则a ︰b=________________.
[提示]a+b=4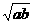 ,即
,即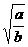 +
+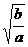 =4令
=4令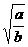 =x,则x+
=x,则x+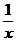 =4即x2-4 x+1=0,解得x=2±
=4即x2-4 x+1=0,解得x=2±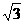 而x=
而x=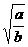 >1,∴ x=2+
>1,∴ x=2+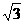 .
.
[答案]7+4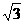 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com