
题目列表(包括答案和解析)
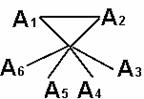
8.设六个圆的圆心分别为A1、A2……A6,假设点P同时在它们的内部,依题意得PA1<A1A2,PA2<A1A2
∴ 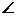 A1PA2为
A1PA2为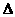 A1PA2 的最大内角 ∴
A1PA2 的最大内角 ∴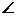 A1PA2>60°,同理可证
A1PA2>60°,同理可证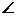 A2PA3>60°,∴……
A2PA3>60°,∴……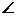 A6PA1>60°
A6PA1>60°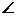 A1PA2+……+
A1PA2+……+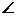 A6PA3+…+
A6PA3+…+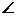 A6PA1>360°,与周角定义相矛盾,故点P不能同时在这六个圆的内部。
A6PA1>360°,与周角定义相矛盾,故点P不能同时在这六个圆的内部。
7. 假设
假设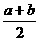 <
<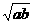 ,则a+b<2
,则a+b<2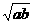 ),(
),(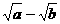 )2<0这与(
)2<0这与(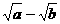 )2
)2
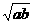
 0,相矛盾
0,相矛盾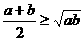 ,其中等号成立的充要条件是a=b。
,其中等号成立的充要条件是a=b。
6.(1)必要性:若ax2-ax+1>0对x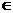 恒成立,由二次函数性质有:
恒成立,由二次函数性质有: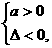
即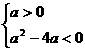 ∴0<a<4
∴0<a<4
(2)充分性:若0<a<4,对函数y=ax2+ax+1,其中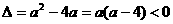 且a>0 ∴ax2-ax+1>0(X
且a>0 ∴ax2-ax+1>0(X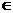 R)恒成立。
R)恒成立。
由(1)(2)命题得证。
5. (1)充分性: a+b+c=0, ∴a·12+b·1+c=0, ∴x=1是方程ax2+bx+c=0的一个根
(2)必要性:
a+b+c=0, ∴a·12+b·1+c=0, ∴x=1是方程ax2+bx+c=0的一个根
(2)必要性: x=1是方程ax2+bx+c=0的根,∴a·12+b·1+c=0,即a+b+c=0综合(1)(2),关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0
x=1是方程ax2+bx+c=0的根,∴a·12+b·1+c=0,即a+b+c=0综合(1)(2),关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0
4.不正确
 a<-b<1, ∴a+b<0且b+1>0
a<-b<1, ∴a+b<0且b+1>0
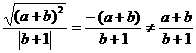
3.假设存在整数m、n使得m2=n2+1998,则m2-n2=1998,即(m+n)(m-n)=1998。
当m与n同奇同偶时,m+n,m-n 都是偶数,∴ (m+n)(m-n)能被4整除,但4不能整除1998,此时(m+n)(m-n)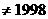 ;
;
当m,n为一奇一偶时,m+n 与m-n 都是奇数,所以(m+n)(m-n)是奇数,此时(m+n)(m-n) 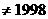 。
。
∴假设不成立则原命题成立。
2.由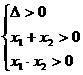 即
即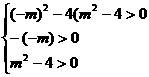 得
得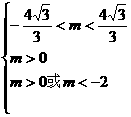 ∴
∴ 2<m<
2<m<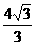
1.(1)“若a是正数,则a的平方根不等于0”逆命题是:“若a的平方根不等于0,则a是正数”,否命题是“若a不是正数,则它的平方根等于0,”逆否命题:“若a的平方根等于0,则a不是正数”。
(2)“若平行四边形的两条对角线不相等,则它不是矩形”,逆命题是:“若平行四边形不是矩形,则它的两条对角线不相等”,否命题是“若平行四边形的两条对角线相等,则它是矩形逆否命题是:“若平行四边形是矩形,则它的两条对角线相等。”
4.充分而不必要条件 5. ABC是等腰直角三角形 6.不内接于圆的四边形对角不互补 7.a=b,或a=-b或
ABC是等腰直角三角形 6.不内接于圆的四边形对角不互补 7.a=b,或a=-b或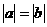 8.若x
8.若x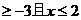 ,则x2+x-6
,则x2+x-6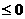 9.充分必要条件 10.0;4;原命题、逆命题、否命题、逆否命题
9.充分必要条件 10.0;4;原命题、逆命题、否命题、逆否命题
1.p且q,p或q,非p 2.a+b不是偶数,则a、b不都是奇数 3.必要而不充分条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com