
题目列表(包括答案和解析)
重点:
正弦定理、余弦定理的推导及运用。
难点:
(1)正弦定理、余弦定理的推导过程;
(2)应用正弦定理、余弦定理解斜三角形。
[学法指导]
学习本节知识时可采用向量法、等积法(面积相等)等不同方法来推导正弦定理,以加深对定理的理解和记忆,由于已知两边及其中一边的对角,不能唯一确定三角形,此时三角形可能出现两解、一解、无解三种情况,因此解此类三角形时,要注意讨论。
深刻领会向量的三角形法则及平面向量的数量积是用向量法推导余弦定理的关键。注意余弦定理的每一个等式中都包含四个不同的量,它们分别是三角形的三边和一个角,知道其中的三个量,便可求得第四个量。当有一个角为90°时,即为勾股定理。因此,勾股定理可看作是余弦定理的特例。
正弦定理和余弦定理是解斜三角形和判定三角形类型的重要工具,其主要作用是将已知条件中的边、角关系转化为角的关系或边的关系。一般地,利用公式a=2RsinA,b=2RsinB,c=2RsinC(R为ΔABC外接圆半径),可将边转化为角的三角函数关系,然后利用三角函数知识进行化简,其中往往用到三角形内角和定理A+B+C=π。
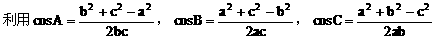
可将有关三角形中的角的余弦转化为边的关系,然后充分利用代数知识来解决问题。在三角形中,有一个角的余弦值为负值,该三角形为钝角三角形;有一个角的余弦值为零,便是直角三角形;三个角的余弦值都为正值,便是锐角三角形。
[例题分析]
例1. 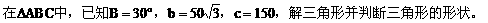
分析:已知两边及一边对角,可用正弦定理先求出c边的对角C,再用内角和定理求出角A,然后用正弦定理求出边a。至于三角形的形状,用角或边均可判断。
解: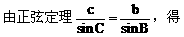
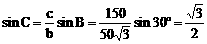
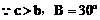
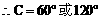
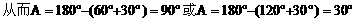
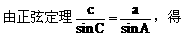
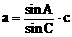
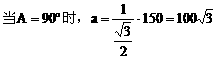
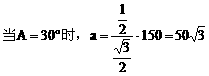
由边(角)的关系易知
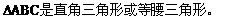
说明:
(1)三角形的形状既可按角分类,又可按边分类,因而判断三角形的形状,既可依角判断,又可依边判断。
(2)正弦定理实际上包含三个等式:
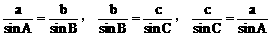
每一个等式都表示了三角形两个角和它们的对边的关系,因此,正弦定理可以用来解决两类解三角形的问题:已知两角和任一边,求其他两边和一角。(此时三角形的形状是确定的,故有唯一解);已知两边和其中一边的对角,求另一边的对角,从而进一步求出其他的边和角(此时不能唯一确定三角形的形状,故要注意解的情况)。
例2. 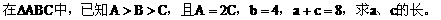
分析:先利用正弦定理及A=2C可用a、c的代数式表示cosC,再利用余弦定理用a、c的代数式表示cosC,即可建立a、c的等量关系式,又a+c=8,解方程组即得a、c。
解: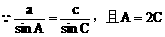
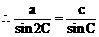
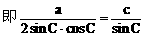
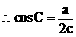
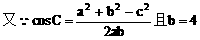
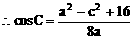
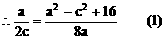
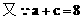
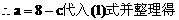
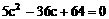
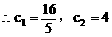
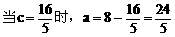
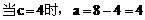
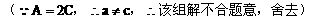
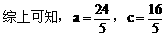
说明:合理利用正、余弦定理及角的关系,寻求边的恒等关系,运用方程的思想是处理此类问题的关键。
例3. 根据下列所给条件,判断ΔABC的形状。
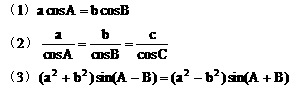
分析:将所给等式中的角换算成边或将边全部转化为角进行判断。
解:(1)方法一:
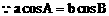
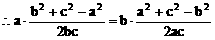
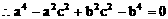
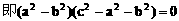
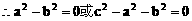
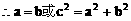
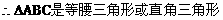
方法二: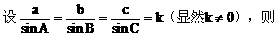
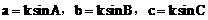
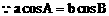
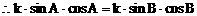
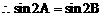
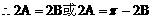
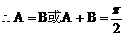
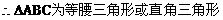
(2)方法一:
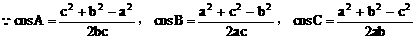
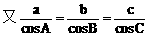
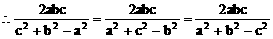
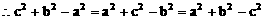
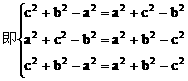
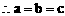
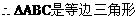
方法二: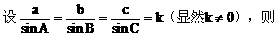
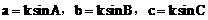
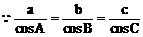
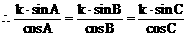

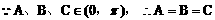
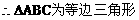
(3)方法一:
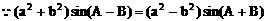
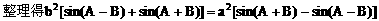
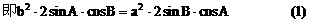
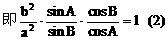
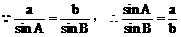
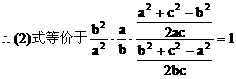
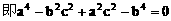
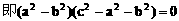
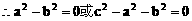
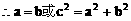
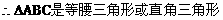
方法二: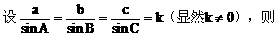
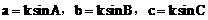
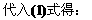
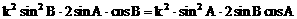
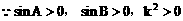
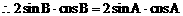
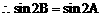
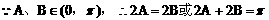
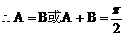
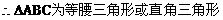
说明:
(1)已知某条件,要判断三角形形状,一般将条件转换成只含边或只含角的式子。
(2)由于三角形各边和它所对角的正弦比相等,故可设比值为一个值k,这时可使解题过程简化。
实际上,这一比值为三角形的外接圆直径2R,即
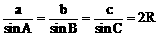
故正弦定理的形式也可写为:
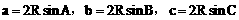
它在解决某些问题时可使解题过程简单化。
例4. 已知圆O的半径为R,它的内接三角形ABC中,

分析:观察已知等式的结构特征可知,先用正弦定理将角转化为边,再用余弦定理求cosC,得出角C后,利用正弦定理,将面积S表示为某角的三角函数形式,再求最值。
解: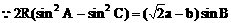
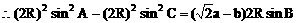
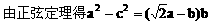
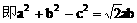
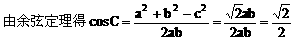
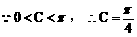
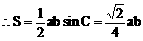
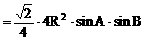
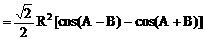
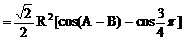
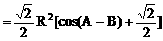

说明:

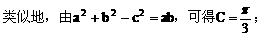
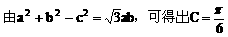
熟记这些结论,可以快速解题。
(2)斜三角形的面积常采用下面公式计算:
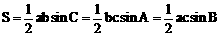
[模拟试题]
§5.9正弦定理、余弦定理
目标:使学生理解正弦定理、余弦定理的证明和推导过程,初步运用它们解斜三角形。并会利用计算器解决解斜三角形的计算问题。培养学生观察、分析、归纳等思维能力、运算能力、逻辑推理能力,渗透数形结合思想、分类思想、化归思想,以及从特殊到一般、类比等方法,进一步提高学生分析问题和解决问题的能力。
5.已知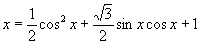 ,则当函数
,则当函数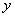 取最大值时,求自变量
取最大值时,求自变量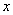 的集合。
的集合。
4.水渠横断面为等腰梯形(如图),渠深为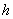 ,梯形面积为S,为了使渠道的渗水量达到最小,应使梯形两腰及下底边长之和为最小,问此时腰与下底夹角
,梯形面积为S,为了使渠道的渗水量达到最小,应使梯形两腰及下底边长之和为最小,问此时腰与下底夹角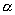 应是多少?
应是多少?

3.已知函数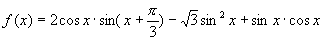
(1)求函数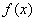 的最小正周期;
的最小正周期;
(2)求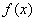 的最大值、最小值;
的最大值、最小值;
(3)求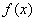 的单调递增区间。
的单调递增区间。
2.求下列函数的定义域。
(1)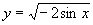 ; (2)
; (2)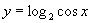 ;
;
(3)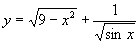 ; (4)
; (4) 。
。
1.判断下列函数的奇偶性。
(1)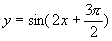 ;
;
(2)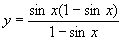 ;
;
(3)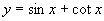 ;
;
(4)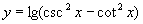 。
。
5.函数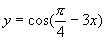 的单调递增区间是 。
的单调递增区间是 。
4.若函数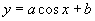 (
(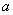 、
、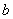 为常数)的最大值为1、最小值为-7,则
为常数)的最大值为1、最小值为-7,则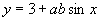 的最大值为 。
的最大值为 。
3.函数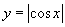 的最小正周期是 。
的最小正周期是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com