
题目列表(包括答案和解析)
7.在矩形ABCD中,O是对角线的交点,若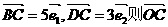 = ( )
= ( )
A.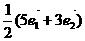 B.
B.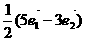 C.
C.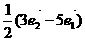 D.
D.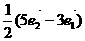
6.下列各量中是向量的是 ( )
A.质量 B.距离 C.速度 D.电流强度
5. 在 ABCD中,设
在 ABCD中,设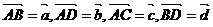 ,则下列等式中不正确的是( )
,则下列等式中不正确的是( )
A.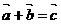 B.
B.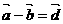
C.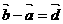 D.
D.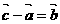
4.已知向量 反向,下列等式中成立的是 ( )
反向,下列等式中成立的是 ( )
A.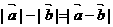 B.
B.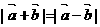
C.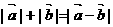 D.
D.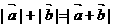
3.在△ABC中,D、E、F分别BC、CA、AB的中点,点M是△ABC的重心,则
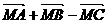 等于 ( )
等于 ( )
A.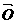 B.
B.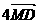 C.
C.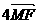 D.
D.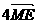
2.下列说法正确的是 ( )
A.方向相同或相反的向量是平行向量
B.零向量的长度为0
C.长度相等的向量叫相等向量
D.共线向量是在同一条直线上的向量
1.如图,已知四边形ABCD是梯形,AB∥CD,E、F、G、H分别是AD、BC、AB与CD
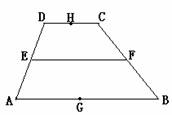 的中点,则
的中点,则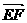 等于 ( )
等于 ( )
A.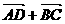 B.
B.
C.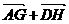 D.
D.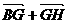
16.解:
∵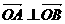 ∴
∴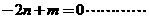 ①……………………
①……………………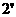
∵A、B、C三点在同一直线上
∴存在唯一的实数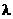 使得
使得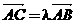 …………………………
…………………………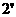
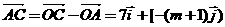 …………………………
…………………………
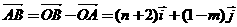 ………………………
………………………
∴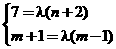 ……………………………………………
……………………………………………
消去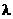 得到
得到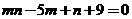 …………②…………………
…………②…………………
由①得到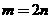 ,代入②解得
,代入②解得
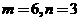 或
或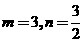
13.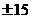 14.
14.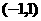 15.②④
15.②④
将物理问题转化成数学问题,利用向量的知识及有关数学方法来解决问题,并解释有关的物理现象。
[学法指导]
向量是既有大小又有方向的量,物理中的很多量都是向量,如力、速度、加速度、位移等。力、速度、加速度、位移的合成与分解就是向量的加法、减法。
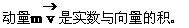

用向量解决物理问题的方法:把物理问题转化为数学问题,抽象成数学模型,对这个数学模型进行探究,进而解释相关物理现象。
[例题分析]
例1. 一条河的两岸平行,河宽为dm,一船从A出发航行到河的对岸,船航行速度大小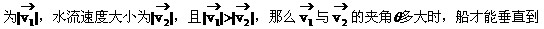 达河岸B处?船航行多少时间?
达河岸B处?船航行多少时间?
分析:如果水是静止的,则船只要取垂直于河岸的方向行驶就行了。但由于水流动的作用,船要被水冲向下游,因此要使船垂直到达对岸,就要使
好垂直于河岸方向。根据题意作出图形,如图(1)。
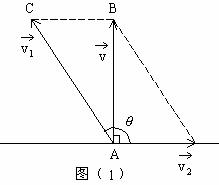

怎样求船航行的时间?用河的宽度除以合速度的大小即得。
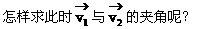
 了。
了。
解:如图(1)

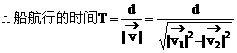
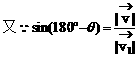
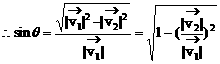
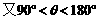
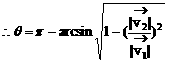
说明:解决此类问题的关键在于“水流速度+航行速度=船的实际速度”,注意“速度”是一个向量,既有大小又有方向。具体计算时要用到解三角形等知识。
例2. 两个粒子a、b从同一源发射出来。在某一时刻,它们的位移分别为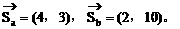

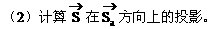
分析:“位移”也是一个向量。粒子b相对于粒子a的位移是什么呢?粒子b相对于粒子a的位移即粒子b与粒子a位移的差向量。
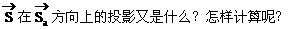
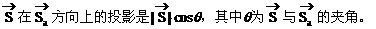
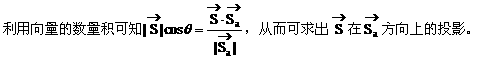
解: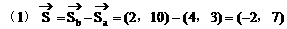
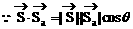
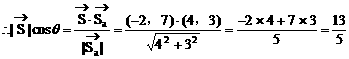
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com