
题目列表(包括答案和解析)
5.当n=1时,a1=S1=1
当n 2时,a1=Sn-Sn-1=3-2n ∴an=3-2n
bn=53-2n
2时,a1=Sn-Sn-1=3-2n ∴an=3-2n
bn=53-2n
∵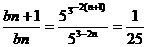 b1=5 ∴{bn}是以5为首项,
b1=5 ∴{bn}是以5为首项,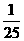 为公比的等比数列。
为公比的等比数列。
∴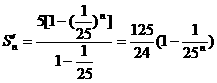
4.设这四个数为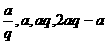
则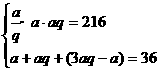
 由①,得a3=216,a=6
③
由①,得a3=216,a=6
③
③代入②,得3aq=36,q=2 ∴这四个数为3,6,12,18
3.∴ a3=3b3 ,  a1+2d=3a1d2 ,
a1+2d=3a1d2 ,  a1(1-3d2)=-2d
①
a1(1-3d2)=-2d
①
 a5=5b5,
a5=5b5,  a1+4d=5a1d4 , ∴a1(1-5d4)=-4d ② ②/①,得
a1+4d=5a1d4 , ∴a1(1-5d4)=-4d ② ②/①,得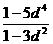 =2,∴ d2=1或d2=
=2,∴ d2=1或d2=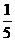 ,由题意,d=
,由题意,d=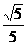 ,a1=-
,a1=-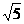 。∴an=a1+(n-1)d=
。∴an=a1+(n-1)d=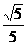 (n-6) bn=a1dn-1=-
(n-6) bn=a1dn-1=-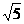 ·(
·(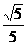 )n-1
)n-1
2.a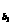 =a1,a
=a1,a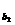 =a10=a1+9d,a
=a10=a1+9d,a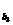 =a46=a1+45d
=a46=a1+45d
由{abn}为等比数例,得(a1+9d)2=a1(a1+45d)得a1=3d,即ab1=3d,ab2=12d,ab3=48d.
∴q=4 又由{abn}是{an}中的第bna项,及abn=ab1·4n-1=3d·4n-1,a1+(bn-1)d=3d·4n-1
∴bn=3·4n-1-2
1. Sn=a1+a2+…+an=(31+21+1)+(32+22+3)+
…+[3n+2n+(2n-1)]=(31+32+…+3n)+(21+22+…2n)++[1+3+…+(2n-1)]=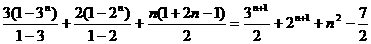
10.(5,7)
规律:(1)两个数之和为n的整数对共有n-1个。(2)在两个数之和为n的n-1个整数对中,排列顺序为,第1个数由1起越来越大,第2个数由n-1起来越来越小。设两个数之和为2的数对方第1组,数对个数为1;两个数之和为3的数对为第二组,数对个数2;…… ,两个数之和为n+1的数对为第n组,数对个数为 n。
∵ 1+2+…+10=55,1+2+…+11=66
∴ 第60个数对在第11组之中的第5个数,从而两数之和为12,应为(5,7)
第60个数对在第11组之中的第5个数,从而两数之和为12,应为(5,7)
5. log2(n+2) 6. (-1)n-1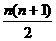 7. n2+n 8. 978 9.
7. n2+n 8. 978 9. 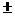 6
6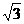
4. 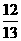
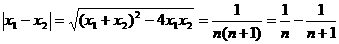
1. 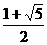 2.
2. 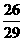 3.
3. 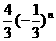
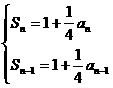 ,相减得an=
,相减得an=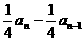 故an=-
故an=-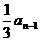
20.(A)an=pn+q(q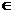 R) (B)a=0,若b=0,不为等比数列 (C) a
R) (B)a=0,若b=0,不为等比数列 (C) a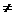 0、b
0、b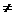 0
0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com