
题目列表(包括答案和解析)
7、使|x-4|+|x-5|<a有实数解的a的取值范围是
A.a >9 B.1<a <9 C.a >1 D.a ≥ 1
6、下列不等式正确的是.
(A)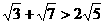 (B)
(B)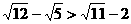
(C)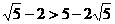 (D)
(D) 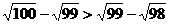
5、已知a<0,-1<b<0,则a, ab, ab 之间的大小关系是
之间的大小关系是
A. a>ab> ab B. ab
B. ab >ab>a C.
ab>a> ab D. ab> ab
>ab>a C.
ab>a> ab D. ab> ab >a
>a
4、不等式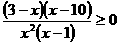 的解集是
的解集是
(A)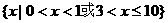 (B)
(B)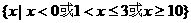
(C)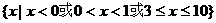 (D)
(D)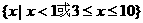
3、设Sn是等差数列{an}的前n项和,已知S6=36,Sn=324,Sn-6=144(n>6),则n等于
A.15 B.16 C.17 D.18
2、若a>b,c<d,则下列结论中不成立的是
A. a-c>b-c B. a-d>b-c C. a+d>b+c D. a-c>a-d
1、在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8等于
A.45 B.75 C.180 D.300
8.(1)设{an}的公式为q.
bn+1-bn=log3an+1-log3an=log3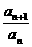 =log3q为常数,做{bn}为等差数列。
=log3q为常数,做{bn}为等差数列。
(2)b1=log3a1=4

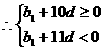
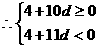
 -
- 。
。
1. Sn=1·( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-3)(
)3+…+(2n-3)( )n-1+(2n-1)(
)n-1+(2n-1)( )n
)n
 Sn=1·(
Sn=1·( )2+3(
)2+3( )3+…+(2n-3)(
)3+…+(2n-3)( )n+(2n-1)(
)n+(2n-1)( )n+1
)n+1
两式相减,得
(1- )Sn=1·(
)Sn=1·( )+2(
)+2( )2+…+2(
)2+…+2( )n-(2n-1)
)n-(2n-1)
( )n+1=2[(
)n+1=2[( )1+(
)1+( )2+…+(…)n]-
)2+…+(…)n]-
 -(2n-1)(
-(2n-1)(  )n+1=
)n+1=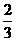 -
- -(2n-1).
-(2n-1).
 即
即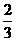 Sn=
Sn=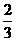 -
-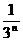 -(2n-1) ·
-(2n-1) ·
 Sn=1-
Sn=1-
6.用an表示该单位第n年花费在轿车上的费用,则
a1=6+36×0.1 a2=6+(36×0.9) ×0.1 a3=(36×0.92) ×0.1
类推可得
an=6+(36×0.9n-1) ×0.1
Sn=a1+a2+…+an=6n+36×0.1×[1+0.9+0.92+…+0.9n-1]=6n+3.6×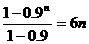 ×+36(1-0.9n)。
×+36(1-0.9n)。
令Sn=36,得n=6×0.9n 0.9n= 。
。
注意到1 n
n 6,取值验证,当n=4时,0.94
6,取值验证,当n=4时,0.94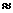 0.6561,
0.6561, ,故n
,故n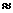 4
4
即使用4年后,花费在轿车上的费用就已达到36万元。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com