
题目列表(包括答案和解析)
5.
 的值为
。
的值为
。
4.已知  ,那么
,那么 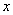 的范围是
。
的范围是
。
3.函数 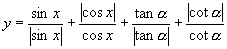 的值域为(
)
的值域为(
)
A. 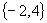 B.
B. 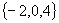
C. 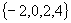 D.
D. 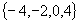
2.下列各式为正号的是( )
A. 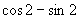 B.
B. 
C. 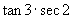 D.
D. 
1.若角 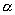 的终边经过点P(
的终边经过点P( 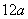 ,
, 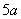 )(
)( 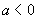 ),则下列计算正确的是(
)。
),则下列计算正确的是(
)。
A. 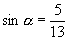 B.
B. 
C. 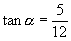 D.
D. 
4、解:由y=cos2x-asinx+b
得 y=-sin2x-asinx+1 令t=sinx(-1≤t≤1)
则y=-t2-at+b+1=-(t+)2+ +b+1
①当0<a≤2 时
-(t+ )2最大值为0,最小值为(1+ )2
+b+1=0 -a+b=4 ∴a=2 a=-6 b=-2 b=-10(舍去)
3、解:设非零x1为第一方程的根 ∴ <x1为第二方程的根
∴ x12-4x1cos2θ+2=0 ①
2()2+4()sin2θ+2-1=0 ② 由②得:-x12+4x1sin2θ+2=0 ③
①+③得:4x1(cos2θ-sinθ)=4
即 =cos2θ-sin2θ代入②得
2(cos2θ-sin2θ)2+4sin2θ(cos2θ-sin2θ)-1=0
即2(1-2sin2θcos2θ)+4sin2θ-4sin22θ-1=0
∴sin2θ±
∵0<2θ<2π
∴2θ= ,π- ,π+ ,2π-
即θ=,,,
1(1)原式=+ +cos2αcsc2α
=cos2α+sin2α+cos2αcsc2α
=1+ctg2α
=csc2α
(2)解:由sin(α+ )=-
∴cosα=-
∵sin2α>0
∴2kπ<2α<2kπ+π
kπ<αkπ+ (k∈z)
∴α为第一象限或第二象限的角
∵cosα=- <0
∴α为第三角限角
sinα=-=
tg = =
2、解:由已知sinx≥
∴ x≤2kπ+
tgx≤-1
∴kπ+ <x≤kπ+
∴2kπ+ <x≤2kπ+ (k∈z)
在此范围内y= 是递减函数
∴当x=2kπ+ 时 (k∈z)
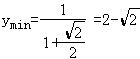
∵它义域为左开右闭区间
∴不存在最大值
4、(kπ- ,kπ+ ) (k∈z)
3、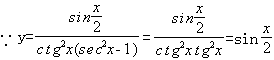
∴T= =4π
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com