9.函数y=2^－|x－1|－m的图象与x轴有交点时，m的范围是(　　 )

A.－1≤m<0　　　　　　　　　　　　　　　 B.0≤m≤1

C.m≥1　　　　　　　　　　　　　　　　　 D.0<m≤1

[解析]令2^－|x－1|－m=0即m=2^－|x－1|

由－|x－1|≤0,得0<2^－|x－1|≤1,即0<m≤1.

[答案]D

8.函数f(x)在区间[1，4]上是减函数，且f(-x)=f(x)，下列不等式成立的是(　 )

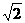A.f()>f(-)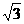

B.f(-1)<f(3)

C.f(-π)>f(π)

D.f(2)<f(-3)

[答案]A

7.设a=log_0.70.8,b=log_1.10.9,c=1.1^0.9，则(　　 )

A.a<b<c　　　　　　　　　　　　　　　　 B.b<c<a

C.b<a<c　　　　　　　　　　　　　　　　 D.c<a<b

[解析]∵log_1.10.9<0<log_0.70.8<1<1.1^0.9,∴b<a<c

[答案]C

6.函数y=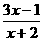的图象一定(　　 )

A.关于点(－2，3)对称　　　　　　　　　　 B.关于点(2，－3)对称

C.关于直线x=－2对称　　　　　　　　　　 D.关于直线y=－3对称

[解析]由y=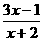=3－.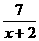

[答案]A

5.函数f(x)的图象如图2-31所示，则不等式xf(x)＞0的解集是(　　 )

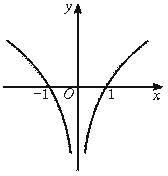
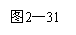
A.(－∞，－1)∪(0，1)　　　　　　　　　　　 B.(－1，0)∪(1，+∞)

C.(－∞，－1)∪(1，+∞)　　　　　　　　 D.(－1，0)∪(0，1)

[解析]xf(x)＞0

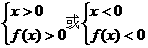
由图象知f(x)＞0x＜－1或x＞1，f(x)＜0－1＜x＜0或0＜x＜1

∴xf(x)＞0x＞1或－1＜x＜0.

[答案]B

4.设F(x)=lnx,f(x)=1－x²,则函数g(x)=F［f(x)］的定义域是(　　 )

A.(0,+∞)　　　　　　　　　　　　　　　 B.(－∞,+∞)

C.{x｜x∈R且x≠±1}　　　　　　　 D.(－1，1)

[解析]1－x²＞0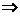|x|＜1,

∴x∈(－1,1).

[答案]D

3.若f(x)=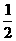(e^x－e^－x),g(x)= 　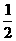(e^x+e^－x),则f(2x)等于(　　 )

A.2f(x)　　　　　　　　　　　　　　 B.2g(x)

C.2［f(x)+g(x)］　　　　　　　　　　 D.2f(x)·g(x)

[解析]2f(x)·g(x)=2·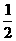(e^x－e^－x)·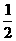(e^x+e^－x)= 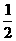(e^2x－e^－2x)=f(2x).

[答案]D

2.已知f(x)=x+1,若f(x+1)的图象关于直线x=2对称图象对应的函数为g(x)，则g(x)为(　　 )

A.6－x　　　　　 B.x－6　　　　　　　 C.x－2　　　　　 D.－x－2

[解析]由f(x)=x+1可得f(x+1)=x+2，f(x+1)的图象关于x=2对称的图象对应的函数g(x)=　　　 6－x.

[答案]A

1.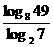的值是(　　 )

A.2　　　　　　 B.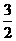　　　　　　　　 C.1　　　　　　 D.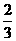

[解析]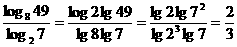

[答案]D

12．(1)试用万能公式证明：.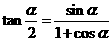

　 (2)已知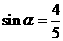，当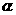为第二象限角时，利用(1)的结论求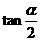的值.