7. 函数y=sin2x的图像向左平移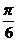所得曲线的对应函数式(　　 )

A.y=sin(2x+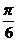)　　 B.y=sin(2x-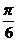)　C.y=sin(2x+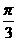) 　D.y=sin(2x-)

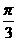6．函数y=Acos(ωx+φ)(A≠0,ω≠0)的奇偶性(　　 )

A.仅与A有关　　　 B.仅与ω有关　C.仅与φ有关　　　　 D.与A、ω、φ有关

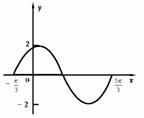
5．如图是函数y=Asin(ωx+φ)图像一段，函数定义域是　　　　 ，值域是　　　　 ，周期是　　　　 ，振幅是　　　　 ，函数解析式是　　　　 ，当x=　　　　 时y取最大值=　　　　 ，当x=　　　　 ,y取最小值　　　　 ，x=　　　　 时，y=0，函数递减区间是　　　　 .

4．函数f(x)的横坐标伸长到原来的两倍，再向左平移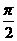个单位，所得到的曲线是y=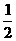sinx的图像，试求函数y=f(x)的解析式.

3．指出将y=sinx的图像变换为y=sin(2x+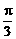)的图像的两种方法.

2．试说明y=cosx的图像经怎样的变换可得到y=3cos(3x+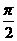)+1的图像?

1．请用五点法作出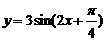在一个周期上的简图

3.y=Asin(ωx+φ)(A＞0，ω＞0)与简谐振动

在物理学中，y=Asin(ωt+φ)(A＞0,ω＞0),其中t∈［0，+∞)，表示简谐振动的运动方程.这时参数A，ω，φ有如下物理意义：

A称为振幅，它表示振动时物体离开平衡位置的最大距离.

T=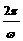称为周期，它表示振动一次所需的时间(亦即函数y的最小正周期).

f=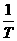= 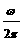称为振动的频率，它表示单位时间内往复振动的次数，ωt+φ叫做相位，当t=0时的相位，即φ称为初相.

2．设f、t、h分别表示相位变换，周期变换，振幅变换，变换作图法共有以下不同的程序：

(1)f→t→h;(2)f→g→t(3)t→h→f;(4)t→f→h;(5)h→f→t;(6)h→t→f

1．函数y=Asin(ωx+φ)的图像与y=sinx的图像关系.

(1)振幅变换：函数y=Asinx(A＞0,且A≠1)的图像，可以看作是y=sinx图像上所有点的纵坐标伸长(A＞1)或缩短(0＜A＜1)到原来的A倍(横坐标不变)而得到的.这种变换叫振幅变换，它实质上是纵向的伸缩.

(2)周期变换：函数y=sinωx(ω＞0,且ω≠1)的图像，可以看作是把y=sinx的图像上各点的横坐标都缩短(ω＞1)或伸长(0＜ω＜1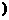到原来的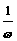倍(纵坐标不变)而得到的，由y=sinx的图像变换为y=sinωx的图像，其周期由2π变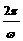.这种变换叫做周期变换.它实质上是横向的伸缩.

(3)相位变换：函数y=sin(x+φ)(φ≠0)的图像，可以看作是把y=sinx的图像上各点向左(φ＞0)或向右(φ＜0)平移｜φ｜个单位而得到的.这种由y=sinx的图像变换为y=sin(x+φ)的图像的变换，使相位x变为x+φ,我们称它为相位变换.它实质上是一种左右平移变换.

应用振幅变换、周期变换、相位变换(左右平移变移)和上下平移变换可由y=sinx的图像得到y=Asin(ωx+φ)+k的图像.