
题目列表(包括答案和解析)
3.若∣a+b∣=∣a∣+∣b∣成立,则 ( )
A. a=λb (λ R)
B. a=λb (λ>0)
R)
B. a=λb (λ>0)
C. a=λb (λ<0)
D. a=λb (λ 0)或a=0
0)或a=0
2.已知o是平行四边形ABCD对角线的交点,则下面结论正确的是( )
A. 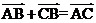 B.
B. 
C.  D.
D.  0
0
1.下列命题中正确的是 ( )
A. 若两个向量相等,则它们的起点和终点分别重合;
B. 模相等的两个平行向量是相等向量;
C. 若a和b都是单位向量,则a=b;
D. 两个相等向量的模相等;
22、解法二:由题意得:sin2θ-2msinθ+2m+1>0对θ∈R恒成立
令t=sinθ ∴t∈[-1,1]
令g(t)=t2-2mt+2m+1=(t-m)2+m2+2m+1,t∈[-1,1]
若m<-1,要g(t)>0恒成立,则一定有g(-1)>0,
|
|
 m<-1
m<-1
g(-1)>0
若-1≤m≤1,要使g(t)>0恒成立,则一定有g(m )>0,
|
|
 -1≤m≤1
-1≤m≤1
g(m)>0
若m>1,要使g(t)>0恒成立,则一定有g(1 )>0,
|
|
 m>1
m>1
g(1)>0
综上所述:当m>1-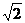 时,对θ∈R时,原不等式恒成立
时,对θ∈R时,原不等式恒成立
22、解法一:由题cos2θ-2<2m-2msinθ即:cos2θ-2<2m(1-sinθ) θ∈R恒成立
当sinθ=1时 cos2θ-2<0 恒成立;当sinθ≠1时 1-sinθ>0
∴2m> 设y=
设y= 令1-sinθ=t
令1-sinθ=t
y= =
=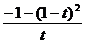 =
= = -(t+
= -(t+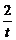 )+2
)+2
又t=1-sinθ∈[0,2]
当t=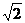 时,(t+
时,(t+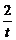 )min=2
)min=2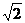 ymax=-2
ymax=-2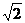 +2
+2
∴2m>2-2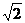 ∴当m>1-
∴当m>1-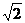 原不等式恒成立
原不等式恒成立
21、解:∵B=π-(A+C)∴sinB=
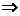 sin[π-(A+C)]=
sin[π-(A+C)]= 
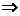 sin(A+C)=
sin(A+C)= 
A<B<C, 0<B< ∴
∴ <A+C<π, ∴cos(A+C)= -
<A+C<π, ∴cos(A+C)= -
0<2A+C<A+B+C=π ∴sin(2A+C)=

cosA=cos[(2A+C)-(A+C)]= - ×(-
×(- )+
)+ ×
× =
=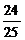
20、证明: 由2sin(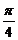 + α)=sinθ+cosθ
+ α)=sinθ+cosθ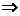
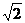 sinα+
sinα+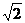 cosα= sinθ+cosθ
cosα= sinθ+cosθ
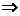 2+4sinαcosα=1+sin2θ ① 2sin2β=sin2θ
②
2+4sinαcosα=1+sin2θ ① 2sin2β=sin2θ
②
②代入①得:2+2sin2α=1+2sin2β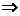 2sin2α=2sin2β-1
2sin2α=2sin2β-1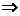 2sin2α=-cos2β
2sin2α=-cos2β
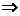 sin2α+
sin2α+ β=0
β=0
19、函数表达式为y=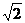 sin(
sin(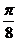 x+
x+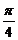 ),振幅A=
),振幅A=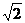 ,频率为
,频率为 ,初相为
,初相为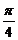 。
。
18、解:f(x)=3 cosx sinx -3cos2x+2=
cosx sinx -3cos2x+2= sin2x -
sin2x - cos2x+
cos2x+ =3sin(2x-
=3sin(2x-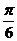 )+
)+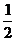
最小正周期T= =π当2x -
=π当2x -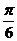 =
=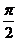 +2kπ即x=kπ+
+2kπ即x=kπ+ ,k∈z时fmax=
,k∈z时fmax=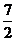 , x的集合
, x的集合
17、①解:  =
= =
= = -1
= -1
②由sin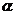 =
= 得cosα= -
得cosα= -
∴原式= =
= = -
= -
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com