
题目列表(包括答案和解析)
8. 已知sin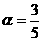 ,
,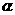 是第二象限的角,且tan(
是第二象限的角,且tan(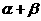 )=1,则tan
)=1,则tan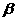 的值为( )
的值为( )
A.-7
B.7
C.-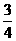 D.
D.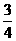
7. 设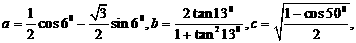 则有( )
则有( )
A.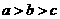 B.
B.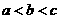 C.
C. 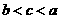 D.
D. 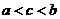
6. 函数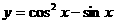 的值域是
( )
的值域是
( )
A、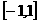 B、
B、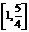 C、
C、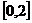 D、
D、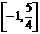
5. 下列函数中,最小正周期为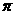 ,且图象关于直线
,且图象关于直线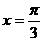 对称的是( )
对称的是( )
A.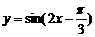 B.
B.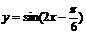 C.
C. D.
D.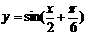
4. 已知函数f(x)=sin(x+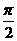 ),g(x)=cos(x-
),g(x)=cos(x-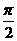 ),则下列结论中正确的是( )
),则下列结论中正确的是( )
A.函数y=f(x)·g(x)的最小正周期为2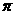 B.函数y=f(x)·g(x)的最大值为1
B.函数y=f(x)·g(x)的最大值为1
C.将函数y=f(x)的图象向左平移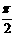 单位后得g(x)的图象
单位后得g(x)的图象
D.将函数y=f(x)的图象向右平移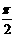 单位后得g(x)的图象
单位后得g(x)的图象
3. 在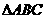 中,①sin(A+B)+sinC;②cos(B+C)+cosA;③
中,①sin(A+B)+sinC;②cos(B+C)+cosA;③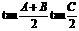 ;④
;④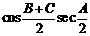 ,其中恒为定值的是( ) A、① ② B、② ③ C、② ④ D、③ ④
,其中恒为定值的是( ) A、① ② B、② ③ C、② ④ D、③ ④
2. 在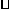 ABCD中,设
ABCD中,设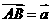 ,
,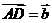 ,
,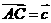 ,
,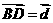 ,则下列等式中不正确的是( )
,则下列等式中不正确的是( )
A.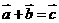 B.
B.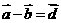 C.
C.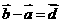 D.
D.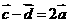
1. 化简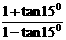 等于 ( ) A.
等于 ( ) A. 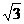 B.
B. 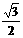 C. 3 D. 1
C. 3 D. 1
22.(1)当a=1,b=-2时,f(x)=x2-x-3=x x2-2x-3=0
x2-2x-3=0 (x-3)(x+1)=0
(x-3)(x+1)=0 x=3或x=-1,∴f(x)的不动点为x=3或x=-1.
x=3或x=-1,∴f(x)的不动点为x=3或x=-1.
(2)对任意实数b,f(x)恒有两个相异不动点 对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根 对任意实数b,Δ=b2-4a(b-1)>0恒成立
对任意实数b,Δ=b2-4a(b-1)>0恒成立 对任意实数b,b2-4ab+4a>0恒成立
对任意实数b,b2-4ab+4a>0恒成立 Δ′=16a2-16a<0
Δ′=16a2-16a<0 0<a<1.
0<a<1.
21.(1)证明:令a=b=0,则f(0)=f 2(0).
又f(0)≠0,∴f(0)=1.
(2)证明:当x<0时,-x>0,
∴f(0)=f(x)·f(-x)=1.
∴f(-x)=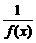 >0.又x≥0时f(x)≥1>0,
>0.又x≥0时f(x)≥1>0,
∴x∈R时,恒有f(x)>0.
(3)证明:设x1<x2,则x2-x1>0.
∴f(x2)=f(x2-x1+x1)=f(x2-x1)·f(x1).
∵x2-x1>0,∴f(x2-x1)>1.
又f(x1)>0,∴f(x2-x1)·f(x1)>f(x1).
∴f(x2)>f(x1).∴f(x)是R上的增函数.
(4)解:由f(x)·f(2x-x2)>1,f(0)=1得f(3x-x2)>f(0).又f(x)是R上的增函数,
∴3x-x2>0.∴0<x<3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com